在S=”abcabcabdabba”中查找T=”abcabd”,如果使用KMP匹配算法,当第一次搜索到S[5] 和T[5]不等后,S下标不是回溯到1,T下标也不是回溯到开始,而是根据T中T[5]==’d’的模式函数值(next[5]=2,为什么?后面讲),直接比较S[5] 和T[2]是否相等,因为相等,S和T的下标同时增加;因为又相等,S和T的下标又同时增加。。。最终在S中找到了T。如图:
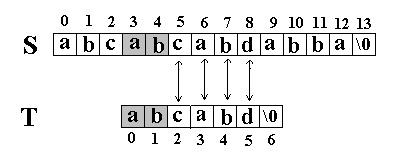
KMP匹配算法和简单匹配算法效率比较,一个极端的例子是:
在S=“AAAAAA…AAB“(100个A)中查找T=”AAAAAAAAAB”, 简单匹配算法每次都是比较到T的结尾,发现字符不同,然后T的下标回溯到开始,S的下标也要回溯相同长度后增1,继续比较。如果使用KMP匹配算法,就不必回溯.
对于一般文稿中串的匹配,简单匹配算法的时间复杂度可降为O (m+n),因此在多数的实际应用场合下被应用。
KMP算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。看前面的例子。为什么T[5]==’d’的模式函数值等于2(next[5]=2),其实这个2表示T[5]==’d’的前面有2个字符和开始的两个字符相同,且T[5]==’d’不等于开始的两个字符之后的第三个字符(T[2]=’c’).如图:
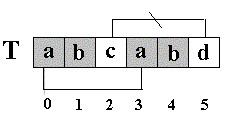
也就是说,如果开始的两个字符之后的第三个字符也为’d’,那么,尽管T[5]==’d’的前面有2个字符和开始的两个字符相同,T[5]==’d’的模式函数值也不为2,而是为0。
前面我说:在S=”abcabcabdabba”中查找T=”abcabd”,如果使用KMP匹配算法,当第一次搜索到S[5] 和T[5]不等后,S下标不是回溯到1,T下标也不是回溯到开始,而是根据T中T[5]==’d’的模式函数值,直接比较S[5] 和T[2]是否相等。。。为什么可以这样?
刚才我又说:“(next[5]=2),其实这个2表示T[5]==’d’的前面有2个字符和开始的两个字符相同”。请看图 :因为,S[4] ==T[4],S[3] ==T[3],根据next[5]=2,有T[3]==T[0],T[4] ==T[1],所以S[3]==T[0],S[4] ==T[1](两对相当于间接比较过了),因此,接下来比较S[5] 和T[2]是否相等。。。
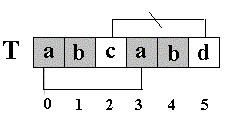
有人可能会问:S[3]和T[0],S[4] 和T[1]是根据next[5]=2间接比较相等,那S[1]和T[0],S[2] 和T[0]之间又是怎么跳过,可以不比较呢?因为S[0]=T[0],S[1]=T[1],S[2]=T[2],而T[0] != T[1], T[1] != T[2],==> S[0] != S[1],S[1] != S[2],所以S[1] != T[0],S[2] != T[0]. 还是从理论上间接比较了。
有人疑问又来了,你分析的是不是特殊轻况啊。
假设S不变,在S中搜索T=“abaabd”呢?答:这种情况,当比较到S[2]和T[2]时,发现不等,就去看next[2]的值,next[2]=-1,意思是S[2]已经和T[0] 间接比较过了,不相等,接下来去比较S[3]和T[0]吧。
假设S不变,在S中搜索T=“abbabd”呢?答:这种情况当比较到S[2]和T[2]时,发现不等,就去看next[2]的值,next[2]=0,意思是S[2]已经和T[2]比较过了,不相等,接下来去比较S[2]和T[0]吧。
假设S=”abaabcabdabba”在S中搜索T=“abaabd”呢?答:这种情况当比较到S[5]和T[5]时,发现不等,就去看next[5]的值,next[5]=2,意思是前面的比较过了,其中,S[5]的前面有两个字符和T的开始两个相等,接下来去比较S[5]和T[2]吧。
总之,有了串的next值,一切搞定。那么,怎么求串的模式函数值next[n]呢?(本文中next值、模式函数值、模式值是一个意思。)
怎么求串的模式值next[n]
定义:
(1)next[0]= -1 意义:任何串的第一个字符的模式值规定为-1。
(2)next[j]= -1 意义:模式串T中下标为j的字符,如果与首字符
相同,且j的前面的1—k个字符与开头的1—k
个字符不等(或者相等但T[k]==T[j])(1≤k<j)。
如:T=”abCabCad” 则 next[6]=-1,因T[3]=T[6]
(3)next[j]=k 意义:模式串T中下标为j的字符,如果j的前面k个
字符与开头的k个字符相等,且T[j] != T[k] (1≤k<j)。
即T[0]T[1]T[2]。。。T[k-1]==
T[j-k]T[j-k+1]T[j-k+2]…T[j-1]
且T[j] != T[k].(1≤k<j);
(4) next[j]=0 意义:除(1)(2)(3)的其他情况。
举例:
01)求T=“abcac”的模式函数的值。
next[0]= -1 根据(1)
next[1]=0 根据 (4) 因(3)有1<=k<j;不能说,j=1,T[j-1]==T[0]
next[2]=0 根据 (4) 因(3)有1<=k<j;(T[0]=a)!=(T[1]=b)
next[3]= -1 根据 (2)
next[4]=1 根据 (3) T[0]=T[3] 且 T[1]=T[4]
即
下标 | 0 | 1 | 2 | 3 | 4 |
T | a | b | c | a | c |
next | -1 | 0 | 0 | -1 | 1 |
若T=“abcab”将是这样:
下标 | 0 | 1 | 2 | 3 | 4 |
T | a | b | c | a | b |
next | -1 | 0 | 0 | -1 | 0 |
为什么T[0]==T[3],还会有next[4]=0呢, 因为T[1]==T[4], 根据 (3)” 且T[j] != T[k]”被划入(4)。
02)来个复杂点的,求T=”ababcaabc” 的模式函数的值。
next[0]= -1 根据(1)
next[1]=0 根据(4)
next[2]=-1 根据 (2)
next[3]=0 根据 (3) 虽T[0]=T[2] 但T[1]=T[3] 被划入(4)
next[4]=2 根据 (3) T[0]T[1]=T[2]T[3] 且T[2] !=T[4]
next[5]=-1 根据 (2)
next[6]=1 根据 (3) T[0]=T[5] 且T[1]!=T[6]
next[7]=0 根据 (3) 虽T[0]=T[6] 但T[1]=T[7] 被划入(4)
next[8]=2 根据 (3) T[0]T[1]=T[6]T[7] 且T[2] !=T[8]
即
下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
T | a | b | a | b | c | a | a | b | c |
next | -1 | 0 | -1 | 0 | 2 | -1 | 1 | 0 | 2 |
只要理解了next[3]=0,而不是=1,next[6]=1,而不是= -1,next[8]=2,而不是= 0,其他的好象都容易理解。
03) 来个特殊的,求 T=”abCabCad” 的模式函数的值。
下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
T | a | b | C | a | b | C | a | d |
next | -1 | 0 | 0 | -1 | 0 | 0 | -1 | 4 |
next[5]= 0 根据 (3) 虽T[0]T[1]=T[3]T[4],但T[2]==T[5]
next[6]= -1 根据 (2) 虽前面有abC=abC,但T[3]==T[6]
next[7]=4 根据 (3) 前面有abCa=abCa,且 T[4]!=T[7]
若T[4]==T[7],即T=” adCadCad”,那么将是这样:next[7]=0, 而不是= 4,因为T[4]==T[7].
下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
T | a | d | C | a | d | C | a | d |
next | -1 | 0 | 0 | -1 | 0 | 0 | -1 | 0 |
如果你觉得有点懂了,那么
练习:求T=”AAAAAAAAAAB” 的模式函数值,并用后面的求模式函数值函数验证。
意义:
next 函数值究竟是什么含义,前面说过一些,这里总结。
设在字符串S中查找模式串T,若S[m]!=T[n],那么,取T[n]的模式函数值next[n],
1. next[n]= -1 表示S[m]和T[0]间接比较过了,不相等,下一次比较 S[m+1] 和T[0]
2. next[n]=0 表示比较过程中产生了不相等,下一次比较 S[m] 和T[0]。
3. next[n]= k >0 但k<n, 表示,S[m]的前k个字符与T中的开始k个字符已经间接比较相等了,下一次比较S[m]和T[k]相等吗?
4. 其他值,不可能。
求串T的模式值next[n]的函数
{
int i=1,j=0;
int len=strlen(s);
nextt[0]=-1;
while(i<len)
{
if(j==-1||s[i]==s[j])
{
++i;
++j;
if(s[i]!=s[j])
nextt[i]=j;
else
nextt[i]=nextt[j];
}
else
j=nextt[j];
}
}
KMP模式匹配
{
int len1=strlen(ss);
int len2=strlen(s);
next(s);
int i=0,j=0;
while(i<len1&&j<len2)
{
if(j==-1||ss[i]==s[j])
{
++i;
++j;
}
else
j=nextt[j];
}
if(j>m)
return i-len2+1;
return 0;
}
KMP 水题:
HDOJ 1711 Number Sequence
http://acm.hdu.edu.cn/showproblem.php?pid=1711
 View Code
View Code 2 #include <cstdio>
3 #include <cctype>
4 #include <cstdlib>
5 using namespace std;
6 int n,m;
7 const int N=1000005;
8 const int M=100005;
9 int nextt[M],a[N],b[M];
10 void next()
11 {
12 int i=1,j=0;
13 nextt[0]=-1;
14 while(i<m)
15 {
16 if(j==-1||b[i]==b[j])
17 {
18 ++i;
19 ++j;
20 nextt[i]=j;
21 if(b[i]!=b[j])
22 nextt[i]=j;
23 else
24 nextt[i]=nextt[j];
25 }
26 else
27 j=nextt[j];
28 }
29 }
30 int kmp()
31 {
32 int i=0,j=0;
33 while(i<n&&j<m)
34 {
35 if(j==-1||a[i]==b[j])
36 {
37 ++i;
38 ++j;
39 }
40 else
41 j=nextt[j];
42 }
43 if(j>=m)
44 return i-m+1;
45 return 0;
46 }
47 int main()
48 {
49 int i,t,s;
50 scanf("%d",&t);
51 while(t--)
52 {
53 memset(a,0,sizeof(a));
54 memset(b,0,sizeof(b));
55 memset(nextt,0,sizeof(nextt));
56 scanf("%d%d",&n,&m);
57 for(i=0;i<n;i++)
58 scanf("%d",&a[i]);
59 for(i=0;i<m;i++)
60 scanf("%d",&b[i]);
61 next();
62 s=kmp();
63 if(!s)
64 puts("-1");
65 else
66 printf("%d\n",s);
67 }
68 return 0;
69
HDOJ 1867 A + B for you again
http://acm.hdu.edu.cn/showproblem.php?pid=1867
/*KMP 函数中,j 的值就是匹配的长度。。。 */
 View Code
View Code 2 #include <cstring>
3 #include <cstdio>
4 const int N=100001;
5 using namespace std;
6 int nextt[N];
7 void next(char s[])
8 {
9 int i=1,j=0;
10 int len=strlen(s);
11 nextt[0]=-1;
12 while(i<len)
13 {
14 if(j==-1||s[i]==s[j])
15 {
16 ++i;
17 ++j;
18 if(s[i]!=s[j])
19 nextt[i]=j;
20 else
21 nextt[i]=nextt[j];
22 }
23 else
24 j=nextt[j];
25 }
26 }
27 int kmp(char ss[],char s[])
28 {
29 int len1=strlen(ss);
30 int len2=strlen(s);
31 next(s);
32 int i=0,j=0;
33 while(i<len1&&j<len2)
34 {
35 if(j==-1||ss[i]==s[j])
36 {
37 ++i;
38 ++j;
39 }
40 else
41 j=nextt[j];
42 }
43 if(i==len1)
44 return j;
45 return 0;
46 }
47 int main()
48 {
49 char str1[N],str2[N];
50 while(~scanf("%s%s",str1,str2))
51 {
52 int x=kmp(str1,str2);
53 int y=kmp(str2,str1);
54 if(x==y)
55 {
56 if(strcmp(str1,str2)>0)
57 {
58 printf("%s",str2);
59 printf("%s\n",str1+x);
60 }
61 else
62 {
63 printf("%s",str1);
64 printf("%s\n",str2+x);
65 }
66 }
67 else if(x>y)
68 {
69 printf("%s",str1);
70 printf("%s\n",str2+x);
71 }
72 else
73 {
74 printf("%s",str2);
75 printf("%s\n",str1+y);
76 }
77 }
78 return 0;
79
