P2115 [USACO14MAR]破坏Sabotage

　　主要思想就是二分答案，关键在于如何判断二分的平均值是否可行。

　　

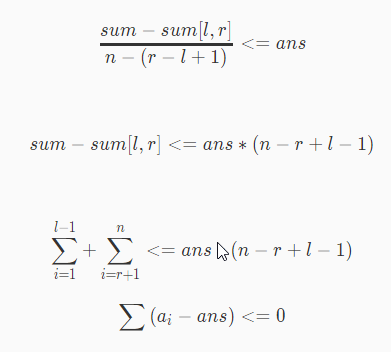
　　在这里之间利用洛谷题解推导过程@communist，因为我没找到这些符号怎么打……

　　ans就是二分的平均值，那么假设存在更好的或者等于的，满足第一个式子，即可得到最后一个。

　　那么只要每一次线性求出每个点对应的最小前缀，最小后缀，判断是否有一组满足最后一个式子即可。

　　O ( n log(n) ) ，加上一点常数。 

　　代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
#define maxn 100005
const double inf=999999999.0;
const double eps=1e-6;
double sumf[maxn],sumb[maxn],mf[maxn],mb[maxn],now[maxn],a[maxn];
int n;
int check(double x)
{
    mf[0]=mf[n+1]=mb[0]=mb[n+1]=inf;
    for(int i=1;i<=n;i++)
    {
        mf[i]=mb[i]=inf;
        now[i]=a[i]-x;
    }
    for(int i=1;i<=n;i++)
    {
        sumf[i]=sumf[i-1]+now[i];
        mf[i]=min(mf[i-1],sumf[i]);
    }
    for(int i=n;i>=1;i--)
    {
        sumb[i]=sumb[i+1]+now[i];
        mb[i]=min(mb[i+1],sumb[i]);
    } 
    for(int i=1;i<=n-2;i++)
        if(mf[i]+mb[i+2]<=0) return 1;
    return 0;
}
int main() 
{
    scanf("%d",&n); 
    for(int i=1;i<=n;i++)
        scanf("%lf",&a[i]);
    double L=1,R=10000;
    double ans;
    while(L+eps<=R)
    {
        double mid=(L+R)/2;
        if(check(mid))
        {
            ans=mid;
            R=mid-eps;
        }
        else L=mid+eps;
    }
    printf("%.3lf
",ans);
    return 0;
}