P4066 [SHOI2003]吃豆豆

　　我和这道题的邂逅，是在那个曼妙的周五的夜晚。

　　作为一道模拟题，她很好地履行了她的职责，不让我会……

　　言归正传…

　　其实在离模拟结束还有14分钟的时候我想出来了费用流的写法……（70分），但是显然我有一段时间没有写网络流了，再加上时间太短，就没有去写。

　　这道题和传纸条好像啊……我一开始考虑dp，但是范围太大了，没法下手……再转念一想——不就是这两条路径上的点最多嘛？而对于不能交叉，我们还能联想到网络流的流量限制。

　　于是——最大费用最大流。

　　对于一个点只能选一次的限制，都是网络流的常规套路了——拆点建边，容量为1，也就是说只有这条边的两端都在最大流上时，费用才能算上。对应的费用（就相当于选了这个点）也为1。对于每一对左下和右上的点，两个点之间连一条流量为1费用为0的边。而对于流量的控制，我们可以建两个源点，s1向s2连一条流量为2的边，这样的话不管出发多少个PACMAN，我们都可以通过控制这条边的容量来实现。

　　我一开始就是按照这个思路，暴力建边，只有70分。因为这样的话边有2000*2000*2+2000*2+2000*2*2条，这太多了……这种稠密图，spfa会受不了的。

　　所以我们考虑优化：

　　对于一个点（红点），我们观察它左下角的点：

　　

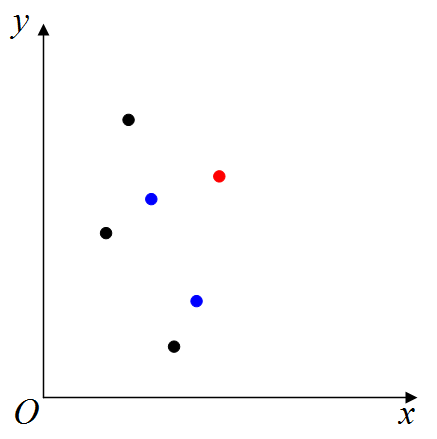
　　我们发现，左下角所有的点，都可以直接或者间接地经过蓝点到达红点。 所以，我们屏蔽掉这两个蓝点与原点构成的矩形中的点，红点只连蓝点。

　　但是有可能存在矩形中的点不走蓝点直接到红点的方法更优，所以我们的中转站——蓝点必须考虑到这钟情况。那么对于一个被拆成两个点的点，它们之间再连一条容量为inf，费用为0的承接边：这就相当于，这个点连接了两个点，这两个点在图上经过这个点连通，但是与这个点无关。

　　也就是说，每一对拆开的点之间有两条（对）边，

#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
#include<vector>
#include<cmath>
using namespace std;
#define maxn 5000005
#define inf 99999999
struct node
{
    int nxt=-1,to,w,flow,cost;
} edge[maxn];
struct xy
{
    int x,y,id;
} po[5000];
int head[maxn],dis[5000],pre[5000];
bool vis[5000];
int s1,s2,t,ans,cnt=-1,n;
bool cmp(xy a,xy b)
{
    if(a.x==b.x) return a.y<b.y;
    return a.x<b.x;
}
void add(int a,int b,int flow,int cost)
{
    edge[++cnt].to=b;
    edge[cnt].w=flow;
    edge[cnt].cost=cost;
    edge[cnt].nxt=head[a];
    head[a]=cnt;
}
int spfa()
{
    for(int i=0; i<=t; i++)
    {
        dis[i]=-inf;
        vis[i]=0;
        pre[i]=-1;
    }
    dis[s1]=0;
    queue<int> Q;
    Q.push(s1);
    vis[s1]=1;
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();
        vis[u]=0;
        for(int i=head[u]; i!=-1; i=edge[i].nxt)
        {
            int v=edge[i].to;
            if(dis[v]<dis[u]+edge[i].cost&&edge[i].w>edge[i].flow)
            {
                dis[v]=dis[u]+edge[i].cost;
                pre[v]=i;
                if(!vis[v])
                {
                    vis[v]=1;
                    Q.push(v);
                }
            }
        }
    }
    if(pre[t]!=-1) return 1;
    return 0;
}
int maxcost_maxflow()
{
    while(spfa())
    {
        int MIN=inf;
        for(int i=pre[t]; i!=-1; i=pre[edge[i^1].to])
        {
            edge[i].flow+=1;
            edge[i^1].flow-=1;
            ans+=edge[i].cost;
        }
    }
    return ans;
}
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d",&n);
    s1=0,s2=2*n+1,t=2*n+2;
    for(int i=1; i<=n; i++)
        scanf("%d%d",&po[i].x,&po[i].y);
    sort(po+1,po+n+1,cmp);
    for(int i=n; i>=1; i--)
    {
        add(i,i+n,1,1);
        add(i+n,i,0,-1);
        add(i,i+n,inf,0);
        add(i+n,i,0,0);
        
        add(s2,i,1,0);
        add(i,s2,0,0);
        add(i+n,t,1,0);
        add(t,i+n,0,0);
        
        int limit_y=0;
        for(int j=i-1; j>=1; j--)
        {
            if(po[j].y<limit_y||po[j].y>po[i].y) continue;
            limit_y=po[j].y;
            add(j+n,i,inf,0);
            add(i,j+n,0,0);
        }
    }
    add(s1,s2,2,0);
    add(s2,s1,0,0);
    printf("%d
",maxcost_maxflow());
    return 0;
}

一条是费用边，一条是承接边。

　　注意：现在两点之间的边容量应该是inf，因为这条边连接的其实是右上角的点和左下角的矩形，我看了半天才发现为啥90……

　　这样边的数量就会大大减少，我们就可以跑spfa了！

　　代码：