计算机组成原理

计算机组成原理 - 第二章 - 运算方法和运算器

1 数据与文字的表示方法

主要分为两种，定点数和浮点数。

1.1 定点数：

约定机器中所有数据的小数点位置是固定不变的。由于约定在固定的位置，小数点就不再用记号.表示。通常将定点数表示成纯小数或纯整数。

假设用n+1位字来表示一个定点数x，其中一位(x_n)用来表示数符，其余位数代表量值。为了将n+1位统一处理，符号位(x_n)放最左侧位置，用0和1分别表示正号和负号。

如果数x表示纯小数，其小数点位于(x_n)和(x_{n-1})之间。

[x_n |. x_{n-1}x_{n-2}...x_1x_0 ]

如果数x表示纯整数，其小数点位于(x_0)之后

[x_n|x_{n-1}x_{n-2}...x_1x_0. ]

下面来分析定点数的数值范围：

应该将数符与尾数分开看。尾数表示该数的绝对值大小，尾数最大即全1，最小即全0。当数符为0时，为正数；数符为1时，为负数。

对于定点整数：$ 0 leq |x| leq 2^n-1$

对于定点小数：(0 leq |x| leq 1-2^{-n})

1.2 浮点数：

浮点表示法，实际上是采用类似于科学计数法的形式来表示数字的一种方法，一个数(N)可以写作(N = 2^e .M)。在计算机中，一个机器浮点数由阶码和尾数及其符号位组成：

[E_s | E_{m-1}...E_{1}E_0 | M_s | M_{n-1}...M_1M_0 ]

其中：

• (E_s)表示阶符
• (E_{m-1}~E_0)表示阶码
• (M_s)表示数符
• (M_{n-1}...M_0)表示尾数

1.3 数的机器码表示

• 原码：正数(x_{原} = x) ，负数(x_{原} = 2^n + |x|)（即符号位为1）
• 反码：正数(x_反=x)，负数(x_{反} = x_{原})符号位不变，其余按位取反
• 补码：正数(x_补 = x)，负数(x_补 = x_反)+1

1.4 浮点数的机器表示

当前的计算机都采用统一的IEEE754标准中的格式表示浮点数。IEEE754标准规定的32位短浮点数和64位长浮点数的标准格式为：

• 32位短浮点数：

  

  若不对浮点数的表示做出明确规定，同一个浮点数的表示就不是唯一的，为了提高数据的表示精度，当尾数的值不为0时，尾数域的最高有效位应为1，这称为浮点数的规格化表示。

  在IEEE754标准中，一个规格化32位浮点数x的真值表示为

  [x = (-1)^S imes (1.M) imes 2^{E-127} ]

  此外，IEEE754还有一些特殊定义：

  • 若E=255且M<>0，则N = NaN
  • 若E=255且M=0，则N=((-1)^Sinfin)
  • 若E=0且M=0，则N=((-1)^S0)
  • 若0<E<255，则N为规格化数
  • 若E=0且M<>0，则N=((-1)^S imes(0.M) imes 2^{E-1023}) 非规格化数

1.5 补码运算

• 补码加法：

  ​ 加法的公式：([x]_{补}+[y]_{补}=[x+y]_补)

  1. 符号位要作为数的一部分一起参与运算
  2. 超过符号位的进位要丢掉

• 补码减法：

  ​ 减法的公式：([x]_{补}-[y]_{补}=[x]_补+[-y]_补)

  ​ 由([y]_{补})求([-y]_{补})的法则是：对([y]_{补})包括符号位按位取反再+1

1.6 溢出

分为上溢（运算结果大于最大正数）和下溢（运算结果小于最小负数）

溢出判别法:

• 进位判别法：判断最高位的进位和符号位的进位是否相同。（即，如果符号位一开始全为0，那么最高位就不得进位；如果符号位一开始全为1，那么最高位就应该进位）
• 采用变形补码，即符号位为两位，正数为00，负数为11，如果运算后得到01或10则发生溢出。

2 运算器设计

2.1 加法器

一位全加器：

[S_i = A_i oplus B_i oplus C_i\ C_{i+1} = A_iB_i + (A_i oplus B_i) C_i ]

延迟运算: 与门、或门 1T；异或门3T

行波进位的补码加法/减法器

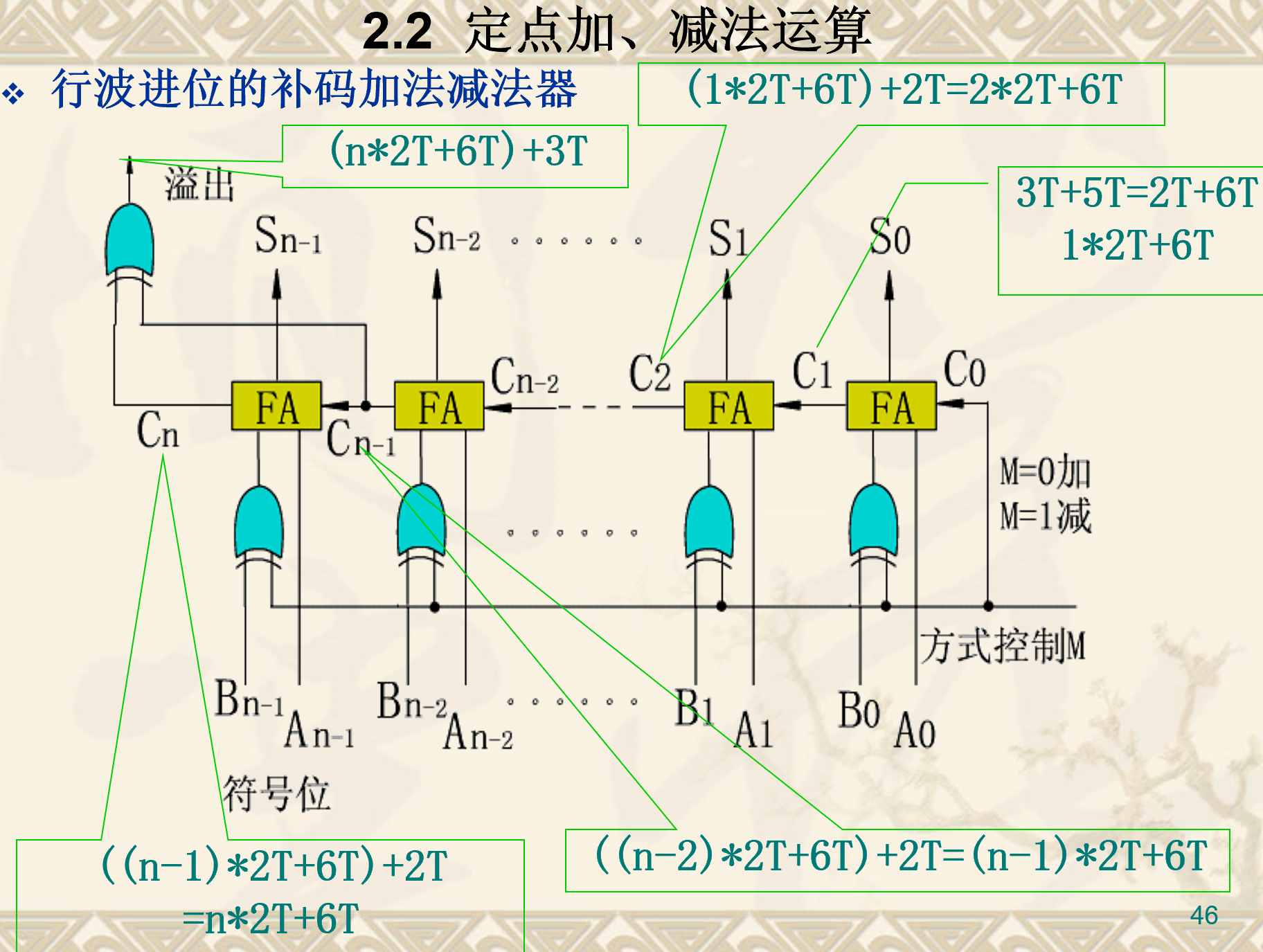
这里简单分析一下：当M=0时，B数各位经过0异或保持原数B不变，最低位进位为0，结果就是A与B相加；当M=1时，B数各位经过1异或取反，再结合最低位的进位1，结果就是A+(-B)= A-B。

2.2 定点乘法

在定点计算机中，两个原码表示的数相乘的运算规则是：乘积的符号位由两数的符号位按异或运算得到，而乘积的数值部分则是两个正数相乘之积。

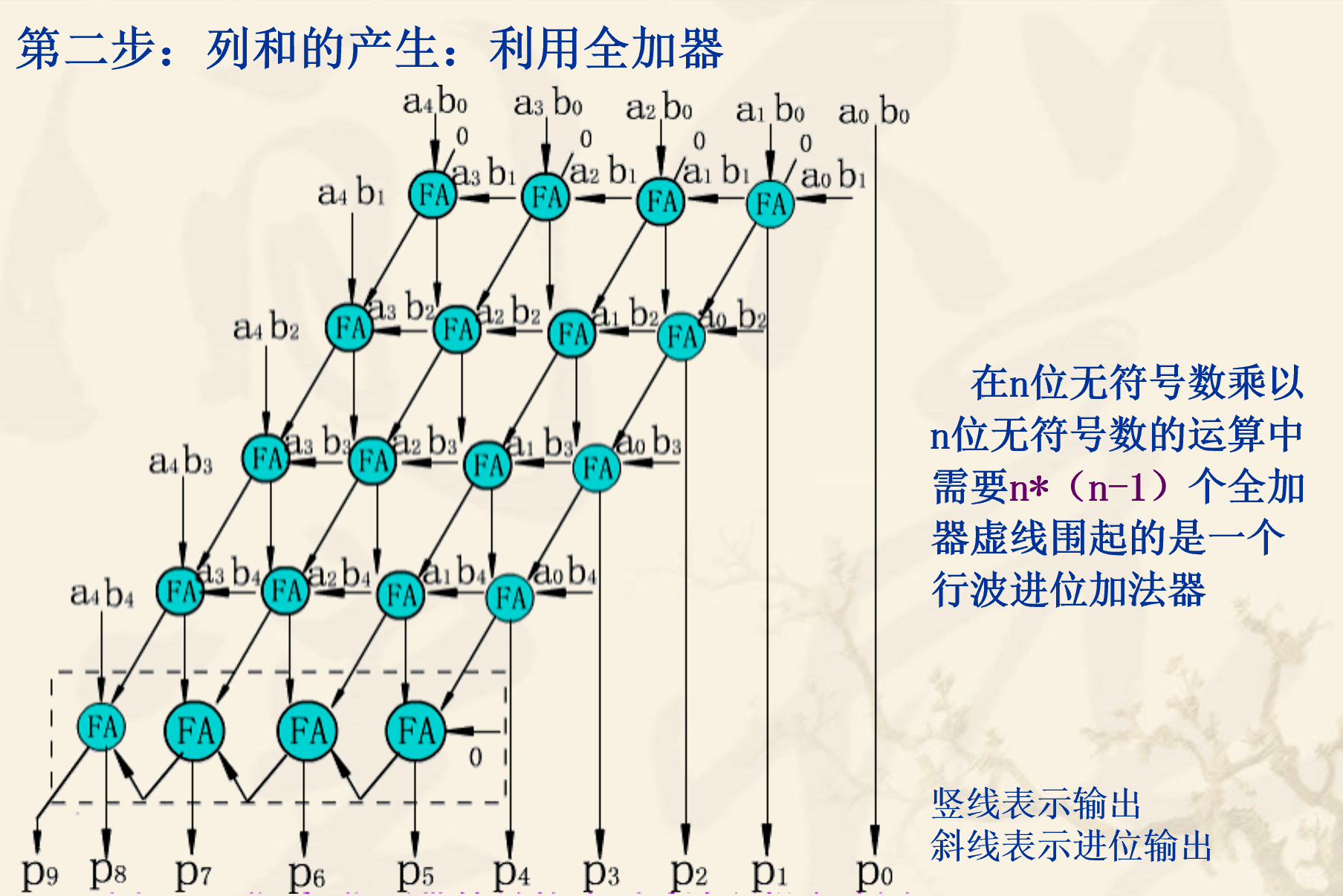
介于串行乘法器已经被淘汰，下面只介绍并行乘法器。并行乘法器的关键是快速产生n*n个位积，然后对位积进行相加运算产生n+n-1个列和。

并行乘法器第一步是并行计算n*n个位积，为此需要n*n个与门；第二步是利用n*(n-1)个全加器计算列和。

2.2.1 间接补码乘法运算

由于在计算机内数据是以补码形式存在，必须考虑补码乘法运算中由补码、原码之间简便的互换运算

由补码直接求原码的运算：

正数的补码不变，负数的补码等于从右边开始遇到的第一个真值的1以后除了符号位以外1变0，0变1。

求补电路的思想：

如果符号位是0，数据不变

如果符号位是1，则符号位保持不变，数据位从lowbit(x)左边除符号位以外全部求反。

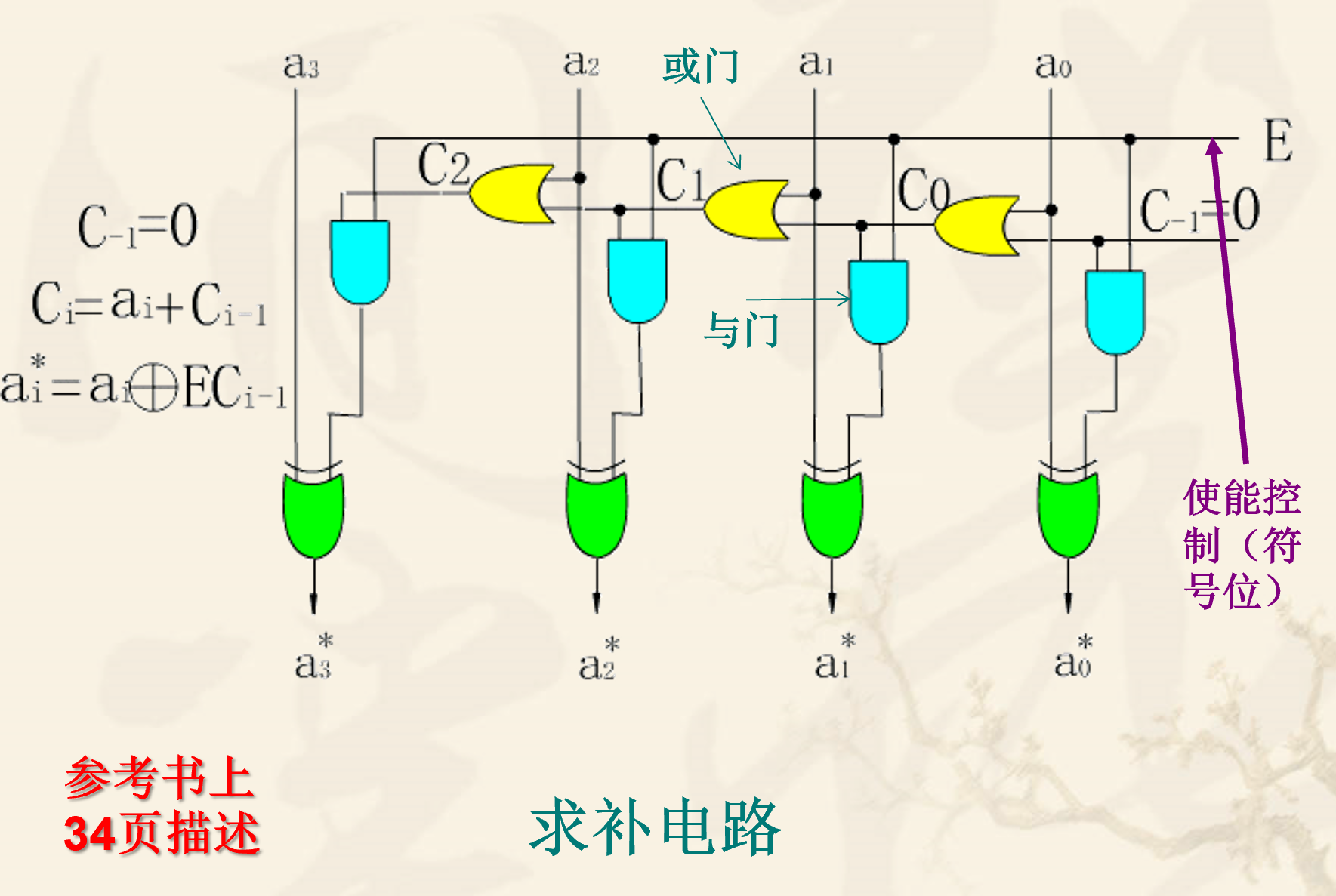
串联的或门陆续接受来自低位的数字和上一次的或门输出，一旦某一次低位数字为1，这一次的或门输出及后续的或门输出均为1。每一级的或门输出都会与使能端E相与，当使能端E=1时，简化为直接由或门输出控制。与门输出接异或门，当或门为1，E=1时，异或门发挥求反功能。当使能端为0时，各级异或门均为0，不发挥求反功能，即各位均保持不变。因此，可以将使能端接数的符号位。

间接补码乘法器，即先将两个数经过算前求补器转化为原码，然后经过乘法器，再将结果经过算后求补器转化为补码。

2.2.2 直接补码乘法运算

根据这一特点，我们可以设计输入带有负权的加法器，用来构造直接补码并行乘法器。根据带有负权的输入端数量，可以分为0，1，2，3四类加法器。用混合加法器构造出的并行乘法器如下图：

3 浮点运算方法和浮点运算器

浮点数的加减法运算分为六个步骤：

• 0操作数检查

  两个操作数中有一个为0，则无需运算

• 比较阶码大小并完成对阶

  两个浮点数进行加减，首先要看两数的阶码是否相同。如果两数阶码不同，表示小数点位置没有对齐，此时必须使二数阶码相同，这个过程称为对阶。对阶操作规定使尾数右移，尾数右移后阶码作相应的增加；因此，对阶时总是小阶向大阶看齐。

• 尾数加减运算

  与定点运算一致

• 结果规格化

  分为左规和右规。这是根据尾数左移和右移来区分的。

• 舍入处理

  在对阶向右规格化，尾数向右移位，这样被右移的尾数的低位部分会被丢掉，从而造成一定误差，要进行舍入处理。

• 判断结果是否溢出

4 总结