GATE tensorflow 1.x 代码解读

看了一些论文的代码，个人感觉 GATE 的代码相对容易读懂一点。本文简单解读一下 GATE 的代码，帮助自己加深理解。为了简洁起见，本文只介绍 inductive 部分，transductive 部分变化不大，不作赘述。由于我是一个 python 和 tensorflow 的小白，本文有些位置会出现关于 python 、tensorflow 1.x 基本语法的介绍。

论文链接：https://arxiv.org/abs/1905.10715
代码链接：https://github.com/amin-salehi/GATE

文件结构：

本文重点讲几个部分：

1. inductive_process.py ：数据读入和预处理
2. inductive_classifier.py ：主程序
3. gate.py ：GATE 模型实现

---

1 inductive_process.py ：数据读入和预处理

inductive-learning 使用到了两个函数：

• load_data:

不用了解此函数内部细节，但要知道参数及返回值：

def load_data(dataset_str): # {'pubmed', 'citeseer', 'cora'}
    """Load data."""
    # ...
	return adj_train, adj, features_train, features, labels, idx_train, idx_val, idx_test

接受指定的数据集名称，返回以下值：

adj_train   	# 1208 * 1208 邻接矩阵; adj_train 是 adj 的子图, 部分节点组成的邻接矩阵
adj 			# 2708 * 2708 邻接矩阵
features_train	# 1208 * 1433 节点属性矩阵; 每一个节点的特征维度都是 1433
features		# 2708 * 1433 节点属性矩阵; 
labels			# 2708 * 7	  各个节点的标签; 每一个标签都是one-hot格式的
idx_train 		# 训练集样本编号 len=140
idx_val 		# 验证集样本编号 len=500
idx_test 		# 测试集样本编号 len=1000

• prepare_graph_data:

此函数将数据进一步处理成模型可以直接使用的格式。首先对传入的邻接矩阵 adj 对角线+1，构成 self-loop，然后转化为 sparse-matrix 的 COO 格式，目的是加速运算和减少内存占用。关于稀疏矩阵的处理，可以参考 这篇文章 。这里暂时忽略稀疏矩阵的细节，也不会影响整体理解。

def prepare_graph_data(adj):
    # adapted from preprocess_adj_bias
    num_nodes = adj.shape[0]
    adj = adj + sp.eye(num_nodes)  # self-loop 稀疏邻接矩阵
    data =  adj.tocoo().data
    adj[adj > 0.0] = 1.0

    if not sp.isspmatrix_coo(adj):
        adj = adj.tocoo() # run

    adj = adj.astype(np.float32)
    indices = np.vstack((adj.col, adj.row)).transpose() # np.vstack 沿着竖直方向堆叠矩阵
    return (indices, adj.data, adj.shape), adj.row, adj.col

该函数返回以下值：

indices: sparse-matrix # 所有非0元素的列坐标和行坐标，即 indices[:,0] 是各个元素的列坐标, indices[:,1] 是各个元素的行坐标。 indices.shape=(3516,2)
adj.data:  	# 每一个非0元素的值, 与 indices 对应。
    		#由于是加了self-loop的邻接矩阵, 转化为sparse-matrix后,全部非0元素的值仍然是1;  shape=(3516,)
adj.shape: # 稀疏矩阵的形状 (1208,1208)
adj.row: # 全部非0元素所在的行号 shape=(3516,)
adj.col: # 全部非0元素所在的列号 shape=(3516,)

2 inductive_classifier.py ：主程序

首先通过函数 parse_args 定义了一系列超参数，可以通过调试得到 args 的值如下：

args=
Namespace(
	dataset='cora',
	dropout=0.0,
	gradient_clipping=5.0,
	hidden_dims=[1433, 512, 512],
	lambda_=1,
	lr=0.0001,
	n_epochs=200
)

args 后期用于传递给训练器，指定训练超参数。

接着，作者给出了 inductive-learning 的训练流程。这里面用到的两个函数 load_data 和 prepare_graph_data 在第一节介绍过，不难理解。重点留意四个位置：

• args.hidden_dims = [feature_dim] + args.hidden_dims

这里 feature_dim = 1433, hidden_dims = [512, 512] 。这里进行 args.hidden_dims = [feature_dim] + args.hidden_dims 的目的是之后定义训练器 trainer 时，需要确定网络结构。输入层维度为 1433 ，两个隐层维度均为 512 。

• Train the Model

这里将 args 作为参数实例化了一个训练器对象 trainer 。然后将训练数据 G_tf, X_train, S, R 通过 trainer.__call__ 传入训练器，进行训练。

• test_embeddings, attentions = trainer.infer(G_tf, X, S, R) 和 Evaluate the quality of embeddings

这里将测试数据传入训练好的模型 trainer 进行 infer ，得到模型输出。GATE 的工作是对图节点进行 embedding 操作，因此我们要对得到的 embedding 进行评估。 将test_embeddings 传入定义好的分类器 classifier ，最终打印结果。

def main(args):
    '''
    Pipeline for Graph Attention Autoencoder.
    '''
    G_train, G, X_train, X, Y, idx_train, idx_val, idx_test = inductive_process.load_data(args.dataset)
    
    # add feature dimension size to the beginning of hidden_dims
    feature_dim = X.shape[1] # feature_dim: 1433
    args.hidden_dims = [feature_dim] + args.hidden_dims # [1433, 512, 512]

    # prepare the train data
    G_tf, S, R = inductive_process.prepare_graph_data(G_train)

    # Train the Model
    trainer = Trainer(args)
    trainer(G_tf, X_train, S, R) # 训练模型

    # prepare the test data

    # 使用完整的图作为数据
    G_tf, S, R = inductive_process.prepare_graph_data(G)

    test_embeddings, attentions = trainer.infer(G_tf, X, S, R)

    # Evaluate the quality of embeddings
    classifier = Classifier(vectors=test_embeddings)
    f1s = classifier(idx_train, idx_test, idx_val, Y, seed=0)
    print(f1s)

3 gate.py ：GATE 模型实现

gate.py 给出了模型的实现，这里自底向上讲解GATE 类的各个函数：

3.1 define_weights(self, hidden_dims)

def define_weights(self, hidden_dims): # [1433,512,512]
    W = {}
    for i in range(self.n_layers):
        W[i] = tf.get_variable("W%s" % i, shape=(hidden_dims[i], hidden_dims[i+1]))
	
    
    Ws_att = {}
    for i in range(self.n_layers):
		v = {}
		v[0] = tf.get_variable("v%s_0" % i, shape=(hidden_dims[i+1], 1))
		v[1] = tf.get_variable("v%s_1" % i, shape=(hidden_dims[i+1], 1))
	Ws_att[i] = v

	return W, Ws_att

此函数用于定义可训练参数 W 和 V，对应于论文这一公式的 (W) 和 (v_s)、(v_r)：

[e_{ij}^{(k)} = Sigmoid(v_s^{(k)^T} sigma(W^{(k)} h_i^{(k-1)}) + v_r^{(k)^T} sigma(W^{(k)} h_j^{(k-1)})) \ ext{where $W^{k} in R^{d^{(k)} imes d^{(k-1)}}$ , $v_s^{(k)} in R^{d^{(k)}}$, $v_r^{(k)}in R^{d^{(k)}}$ are the trainable parameters of the $k^{th}$ encoder layer} ]

每有一个编码层，就会有一个线性变换矩阵 W 和两个线性变换向量 (v_s) 和 (v_r)

3.2 graph_attention_layer(self, A, M, v, layer)

def graph_attention_layer(self, A, M, v, layer): # M = W * H_{k-1}

    with tf.variable_scope("layer_%s"% layer):
        f1 = tf.matmul(M, v[0])
        f1 = A * f1
        f2 = tf.matmul(M, v[1])
        f2 = A * tf.transpose(f2, [1, 0])

        # f1 = v[0] * W * H_{k-1}
        # f2 = ( v[1] * W * H_{k-1} ) ^ T

        logits = tf.sparse_add(f1, f2) # N * N sparse-matrix  E_{ij} 保留邻域注意力(为标准化)

        unnormalized_attentions = tf.SparseTensor(indices=logits.indices,
                                                  values=tf.nn.sigmoid(logits.values),
                                                  dense_shape=logits.dense_shape) # Eij 套一个sigmoid

        attentions = tf.sparse_softmax(unnormalized_attentions) # 套一个softmax归一化

        attentions = tf.SparseTensor(indices=attentions.indices,
                                     values=attentions.values,
                                     dense_shape=attentions.dense_shape)

        return attentions # 返回 tf.SparseTensor N*N 注意力稀疏矩阵

代码还是比较清晰的，传入的 (M) 表示 (W * H_{k-1}) （这是一个令我疑惑的地方：为什么没有对 (W*H_{k-1}) 激活？我仔细看了一下貌似作者忽略了这一步骤，然而论文中有这一步骤），然后仿照 GAT 的代码，先计算 (A * v_s WH_{k-1}) 和 (A * v_r WH_{k-1})， 再做 (f_1 + f_2^T)，利用广播机制得到 (R^{N imes N}) 的 (logits) ，后面的处理请自己看代码注释。最终返回一个 (R^{N imes N}) 的 sparse-matrix 。

3.3 __encoder(self, A, H, layer)

def __encoder(self, A, H, layer):
	H = tf.matmul(H, self.W[layer]) # W * H_{k-1}
	self.C[layer] = self.graph_attention_layer(A, H, self.v[layer], layer) # 完成encoder
	return tf.sparse_tensor_dense_matmul(self.C[layer], H)

【略】

3.4 __decoder(self, H, layer)

def __decoder(self, H, layer):
    H = tf.matmul(H, self.W[layer], transpose_b=True)
    return tf.sparse_tensor_dense_matmul(self.C[layer], H)

注意一点，之前看论文时我以为 decoder 的注意力是独立于 encoder 部分的注意力单独计算的，看代码发现作者是将 decoder 部分沿用 encoder 的注意力。现在想想还是这样更科学，encode-decode 只是对 feature 进行若干次的映射，但节点间的注意力关系应该是固定的，不应该随着 embedding 所在空间表示的改变而改变。

3.5 __init__(self, hidden_dims, lambda_)

def __init__(self, hidden_dims, lambda_):
	self.lambda_ = lambda_ # 1
	self.n_layers = len(hidden_dims) -1 
    # hidden_dims=[1433,512,512] 除去输入层, encoder包括两个编码层 n_layers=2
    self.W, self.v = self.define_weights(hidden_dims) # 返回两个字典W和v, 对应每一层的 W 和 v[0] v[1]
	self.C = {}

【略】

3.6 __call__(self, A, X, R, S)

• python 中 __call__ 方法介绍

__call__() 的作用是使实例能够像函数一样被调用，同时不影响实例本身的生命周期

__call__() 不影响一个实例的构造和析构，但是__call__(),可以用来改变实例的内部成员的值。

def __call__(self, A, X, R, S):
    # Encoder
    H = X
    for layer in range(self.n_layers):
        H = self.__encoder(A, H, layer)

	# Final node representations
	self.H = H

	# Decoder
	for layer in range(self.n_layers - 1, -1, -1):
		H = self.__decoder(H, layer)
    X_ = H

	# The reconstruction loss of node features
	features_loss = tf.sqrt(tf.reduce_sum(tf.reduce_sum(tf.pow(X - X_, 2))))

	# The reconstruction loss of the graph structure
	self.S_emb = tf.nn.embedding_lookup(self.H, S)
	self.R_emb = tf.nn.embedding_lookup(self.H, R)
	structure_loss = -tf.log(tf.sigmoid(tf.reduce_sum(self.S_emb * self.R_emb, axis=-1)))
	structure_loss = tf.reduce_sum(structure_loss)

	# Total loss
	self.loss = features_loss + self.lambda_ * structure_loss

	return self.loss, self.H, self.C

这里给出了 GATE 模型的实现，包括框架部分和 loss 的计算。按照代码默认的参数，self.n_layers=2，表示包含两个 encoder 层和两个 decoder 层。这里重点注意一下 decoder 的构建方式，使用的是递减的 for 循环，表示与 encoder 层轴对称。

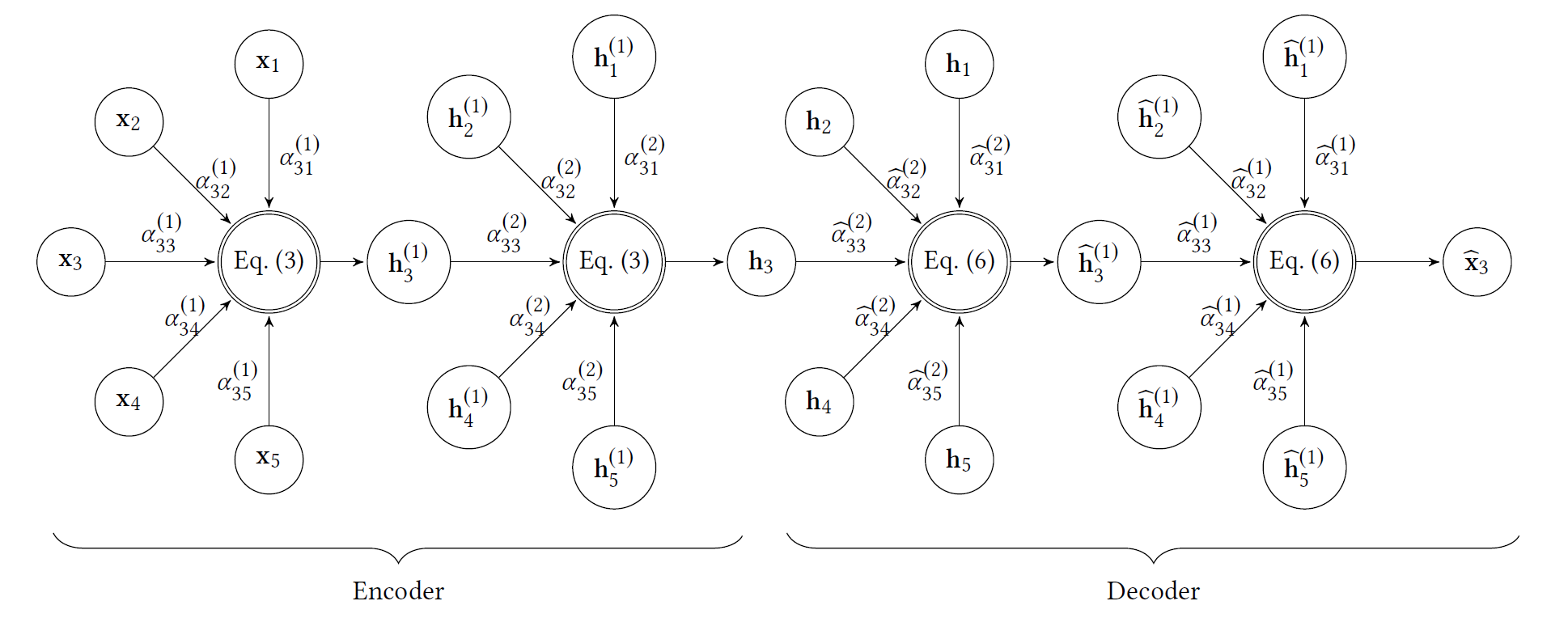
loss 的计算包括图拓扑结构信息和节点特征信息的重构，对应于论文中的这一公式：

[Loss = sum_{i=1}^N||x_i-hat{x}_i||_2-lambda sum_{jin N_i}log(frac{1}{1+exp(-h_i^Th_j)}) ]