题目描述 : https://leetcode-cn.com/problems/trapping-rain-water/
题目描述:
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
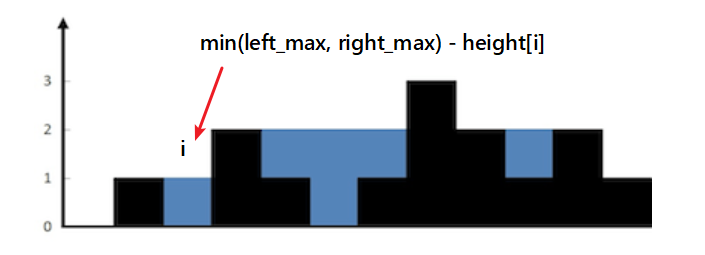
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
思路:
这道题真正难点在于: 在一个位置能容下的雨水量等于它左右两边柱子高度最小值减去它的高度.比如下图所示,
位置i能容下雨水量:min(2,1) - 0 = 1
所以,问题就变成了: 如何找所有位置的左右两边的柱子的最大值?
这里有3种方法:
思路一:动态规划
思路二:双指针
思路三:栈
时间复杂度都是:(O(n))
代码:
思路一:
class Solution:
def trap(self, height: List[int]) -> int:
if not height: return 0
n = len(height)
max_left = [0] * n
max_right = [0] * n
max_left[0] = height[0]
max_right[-1] = height[-1]
# 找位置i左边最大值
for i in range(1, n):
max_left[i] = max(height[i], max_left[i-1])
# 找位置i右边最大值
for i in range(n-2, -1, -1):
max_right[i] = max(height[i], max_right[i+1])
#print(max_left)
#print(max_right)
# 求结果
res = 0
for i in range(n):
res += min(max_left[i], max_right[i]) - height[i]
return res
class Solution {
public int trap(int[] height) {
if (height == null || height.length == 0) return 0;
int n = height.length;
int[] left_max = new int[n];
int[] right_max = new int[n];
left_max[0] = height[0];
int res = 0;
right_max[n - 1] = height[n - 1];
for (int i = 1; i < n; i++) left_max[i] = Math.max(left_max[i - 1], height[i]);
for (int i = n - 2; i >= 0; i--) {
right_max[i] = Math.max(right_max[i + 1], height[i]);
res += Math.min(left_max[i], right_max[i]) - height[i];
}
return res;
}
}
思路二:
class Solution:
def trap(self, height: List[int]) -> int:
if not height: return 0
left = 0
right = len(height) - 1
res = 0
# 记录左右边最大值
left_max = height[left]
right_max = height[right]
while left < right:
if height[left] < height[right]:
if left_max > height[left]:
res += left_max - height[left]
else:
left_max = height[left]
left += 1
else:
if right_max > height[right]:
res += right_max - height[right]
else:
right_max = height[right]
right -= 1
return res
class Solution {
public int trap(int[] height) {
if (height == null || height.length == 0) return 0;
int left = 0;
int right = height.length - 1;
int left_max = 0;
int right_max = 0;
int res = 0;
while (left < right) {
if (height[left] < height[right]) {
if (height[left] < left_max) res += left_max - height[left];
else left_max = height[left];
left++;
} else {
if (height[right] < right_max) res += right_max - height[right];
else right_max = height[right];
right--;
}
}
return res;
}
}
思路三:
class Solution:
def trap(self, height: List[int]) -> int:
if not height: return 0
n = len(height)
stack = []
res = 0
for i in range(n):
#print(stack)
while stack and height[stack[-1]] < height[i]:
tmp = stack.pop()
if not stack: break
res += (min(height[i], height[stack[-1]]) - height[tmp]) * (i-stack[-1] - 1)
stack.append(i)
return res
class Solution {
public int trap(int[] height) {
if (height == null || height.length == 0) return 0;
Deque<Integer> stack = new ArrayDeque<>();
int res = 0;
for (int i = 0; i < height.length; i++){
while ( ! stack.isEmpty() && height[stack.peek()] < height[i]) {
int tmp = stack.pop();
if (stack.isEmpty()) break;
res += (Math.min(height[i],height[stack.peek()]) - height[tmp]) * (i - stack.peek() - 1);
}
stack.push(i);
}
return res;
}
}