codeforce AIM tech Round 4 div 2 B rectangles

2017-08-25 15:32:14

writer：pprp

题目：

B. Rectangles

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given n × m table. Each cell of the table is colored white or black. Find the number of non-empty sets of cells such that:

1. All cells in a set have the same color.
2. Every two cells in a set share row or column.

Input

The first line of input contains integers n and m (1 ≤ n, m ≤ 50) — the number of rows and the number of columns correspondingly.

The next n lines of input contain descriptions of rows. There are m integers, separated by spaces, in each line. The number equals 0 if the corresponding cell is colored white and equals 1 if the corresponding cell is colored black.

Output

Output single integer  — the number of non-empty sets from the problem description.

Examples

input

1 1
0

output

1

input

2 3
1 0 1
0 1 0

output

8

Note

In the second example, there are six one-element sets. Additionally, there are two two-element sets, the first one consists of the first and the third cells of the first row, the second one consists of the first and the third cells of the second row. To sum up, there are 8 sets.

题意说明：

给你 n * m 的矩阵

让你找到有多少符合要求的集合

比如给你一行， 1001011 你可以选择 一个1两个1三个1四个一， 选择0的情况同理，

所以可以看出来用到了组合数的 C(4,1) + C(4,2) + C(4,3) + C(4,4), 

而有如下公式

C(4,0) + C(4,1) + C(4,2) + C(4,3) + C(4,4) =  2 ^ 4

所以公式转化为 2 ^ n - 1(用来计算组合数个个数)

下面的pow函数就是这个功能

之后要横向纵向分别分析，但是这个时候别忘记会重叠，所以减去 n * m

代码如下：

/*
theme: AIM tech Round 4 div 2 B rectangles
writer:pprp
declare:reference from zindow
date:2017/8/25
*/

#include<bits/stdc++.h>

using namespace std;
const int maxn = 60;
typedef long long ll;

//用来计算组合数的
ll pow(int x)
{
    ll res = 1;
    while(x--) res <<= 1;
    return res-1;
}

int main()
{
    int whi = 0, bla = 0;
    int n, m;
    ll ans = 0;
    cin >> n >> m;
    int a[maxn][maxn];

    for(int i = 0 ; i < n ; i++)
        for(int j = 0 ; j < m ; j++)
            cin >> a[i][j];

    for(int i = 0 ; i < n ; i++)
    {
        whi = bla = 0;
        for(int j = 0 ; j < m ; j++)
        {
            if(a[i][j] == 0)whi++;
            else bla++;
        }
        ans += pow(whi) + pow(bla);
    }
    
//    cout << "test" << endl;
//    cout << ans << endl;
    

    for(int j = 0 ; j < m ; j++)
    {
        whi = bla = 0;
        for(int i = 0 ; i < n ; i++)
        {
            if(a[i][j] == 0)whi++;
            else bla++;
        }
//        cout << "case :" << j << "whi" << whi << "bla" << bla << endl;
        ans += pow(whi) + pow(bla);
    }
    
//    cout << "test" << endl;
//    cout << ans << endl;

    cout << ans - m*n << endl;

    return 0;
}

 横向纵向遍历的时候总是出错，

这样记： 初始化的时候 for(i : 1...n)

　　　　　　　　　　　　for(j : 1...m)

一般的这种形式是横向遍历，如果要改成纵向遍历，那么就要内外循环翻转过来

i对应n

j对应m

这样就不容易错了 

另外补充二维数组的知识点，分析的时候就不容易有问题了

 

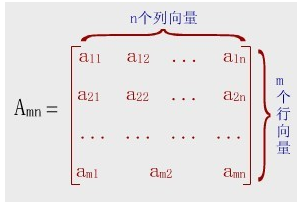
C语言中是按照行优先储存的