LIS学习笔记（两种算法）O(n^2) 和 O(nlogn)

2017-09-02 10:34:21

writer：pprp

最长上升子序列，具体分析看代码：O(n^2)的做法，dp的思想

分析：每次读一个进行扫描，如果当前读入的这个要比之前的大，

说明有可能加一，所以对当前读入这个之前的元素进行扫描，

扫描到的值加上当前这个值跟该出的值进行比对，确定更大的值

关键代码表示如下：

if( i < n && arr[i] < arr[n] )
    f(n) = max(f(i))+ 1;

代码如下：

/*
@theme:LIS最长上升子序列
@writer:pprp
@begin:10:00
@end:10:15
@declare复杂度为O(n^2)
@error:dp[i] = MAX(dp[j]+1,dp[i]),dp[i] = 1初始化为1
@date:2017/9/2
*/

#include <bits/stdc++.h>

using namespace std;

/*
未优化的最长上升子序列
f(i)代表从头到i的位置最长上升子序列的长度
if( i < n && arr[i] < arr[n] )
    f(n) = max(f(i))+ 1;
dp[i]是如果取到arr[i]的时候的最长上升子序列
*/

int dp[10010],arr[10010];

int MAX(int a, int b)
{
    return a > b ? a : b;
}

int main()
{
    int N;
    while(cin >> N && N)
    {
        int max = 0;
        for(int i = 0 ; i < N ;i++)
        {
            dp[i] = 1;
            cin >> arr[i];
            for(int j = 0 ;j < i ; j++)
            {
                if(arr[j] < arr[i])
                    dp[i] = MAX(dp[j] + 1, dp[i]);
            }
            max = MAX(max,dp[i]);
        }
        cout << max << endl;
    }
    return 0;
}

2、采用了优化，记录了可能被选中的点，将其记录在tmp数组中，再从从其中进行查找O(nlog(n))

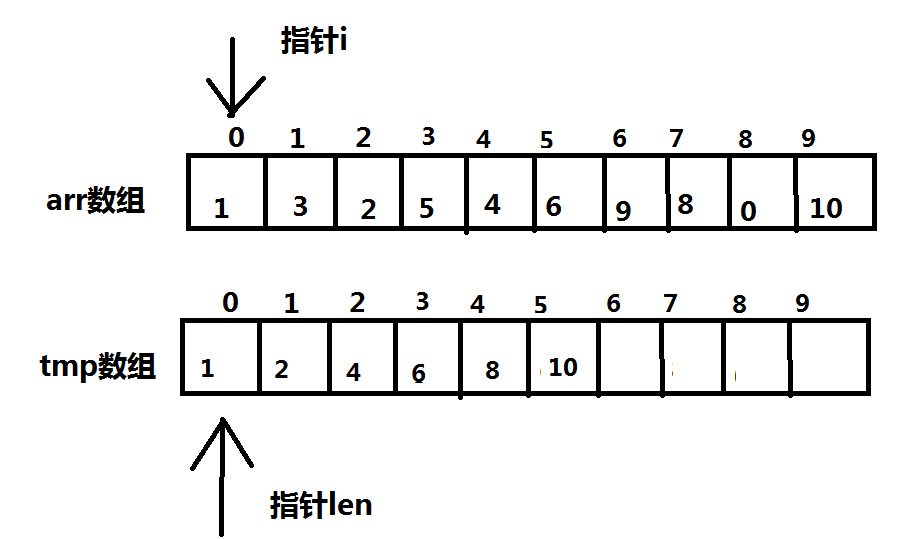
tmp数组中储存的是对于长度i的lLIS他最小可能的结果，当然是这个数越小越容易得到最大结果了...

/*
@theme:tmp最长上升子序列
@writer:pprp
@begin:10:00
@end:14:32
@declare复杂度为O(n^2)
@error:dp[i] = MAX(dp[j]+1,dp[i]),dp[i] = 1初始化为1
@date:2017/9/2
*/

#include <bits/stdc++.h>

using namespace std;

int arr[10010],tmp[10010];
int len;

/*
状态定义：用到tmp数组
tmp[i]:代表的是对于所有长度为i的LIS,他的结果最小有可能是多少，
       如果越小那就越容易被取到
tmp中的元素是严格递增的
状态转移：
        if( dp[j] = i )
            tmp[i] = min(arr[j])
结果查找--用二分的方法去找
if(tmp[i] < arr[n] && tmp[i+1] >= arr[n] )
    f[n] = i+1 .... i 代表的是长度

*/

//二分查找,在tmp中进行二分查找arr[i]
//对tmp数组进行更新
void bisearch(int x)
{
    int left=1,mid,right=len;
    while(left<=right)
    {
        mid=(left+right)>>1;
        if(tmp[mid]<x)
            left=mid+1;
        else
            right=mid-1;
    }
    tmp[left]=x;
}

int main()
{
    int N;
    while(cin >> N && N)
    {
        len=1;
        cin >> arr[0];
        tmp[len]=arr[0];

        for(int i=1; i<N; i++)
        {
            scanf("%d",&arr[i]);

            if(arr[i] > tmp[len])//如果当前i指向的arr的值大于tmp当前的值
            {
                len++;
                tmp[len]=arr[i];
            }//向tmp数组中加入arr的值
            else
                bisearch(arr[i]);//在tmp中进行查找找到的就将其更新
            //如果用lower_bound的话就这样：
            //*lower_bound(tmp,tmp+len,arr[i]) = arr[i];
        }
        printf("%d
",len);
    }
    return 0;
}

 其他图片参考：