01 背包基础

2017-09-03 11:39:16

writer：pprp

以很简单的一个动态规划问题为引入：

从左上角到右下角走过的路径和最大，问你最大为多少？

1、可以想到普通的dp

状态转移为： dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + arr[i][j];

2、采用滚动数组的方式-节约了不必要的空间

状态转移为：dp2[i%2][j] = max(dp2[(i+1)%2][j],dp2[i%2][j-1]) + arr[i][j];

3、采用一维阵列的方式更加节省空间

状态转移为：dp3[j] = max(dp3[j],dp3[j-1]) + arr[i][j];

图解：

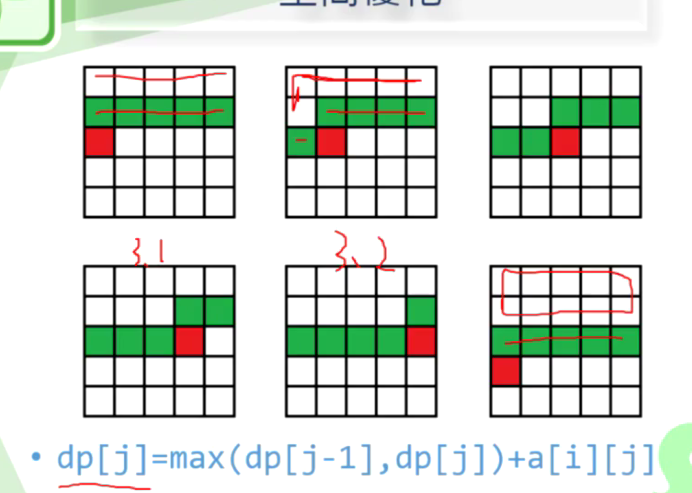
代码如下：

/*
@theme:空间优化,滚动数组，只使用一维阵列
@writer:pprp
@begin:10:45
@end:11:36
@declare:从左上角到右下角的总和最多为多少？
@error:
@date:2017/9/3
*/

#include <bits/stdc++.h>

using namespace std;
const int maxn = 100;
int arr[maxn][maxn];
int dp[maxn][maxn];
int dp2[2][maxn];
int dp3[maxn];
int n, m;

void init()
{
    freopen("in.txt","r",stdin);
    memset(dp,0,sizeof(dp));
    memset(arr,0,sizeof(arr));
    memset(dp2,0,sizeof(dp2));
    memset(dp3,0,sizeof(dp3));
    cin >> n >> m;
    for(int i = 0 ; i < n; i++)
    {
        for(int j = 0 ; j < m ; j++)
        {
            cin >> arr[i][j];
        }
    }
}

//普通简单dp
int fun1()
{
    dp[0][0] = arr[0][0];
    for(int i = 1; i < n ; i++)
    {
        dp[i][0] += arr[i][0] + dp[i-1][0];
    }
    for(int j = 1; j < m ; j++)
    {
        dp[0][j] += arr[0][j] + dp[0][j-1];
    }
    for(int i = 0 ; i < n ; i++)
    {
        for(int j = 0 ; j < m ; j++)
        {
            dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + arr[i][j];
        }
    }

    return dp[n-1][m-1];
}

//滚动数组
int fun2()
{
    dp2[0][0] = arr[0][0];
    for(int i = 1 ; i < m ; i++)
        dp2[0][i] += dp2[0][i-1] + arr[0][i];
    for(int i = 0  ; i < n ; i++)
    {
        for(int j = 0 ; j < m ; j++)
        {
            dp2[i%2][j] = max(dp2[(i+1)%2][j],dp2[i%2][j-1]) + arr[i][j];
        }
    }
    return dp2[(n-1)%2][m-1];
}


//一维阵列
int fun3()
{
    for(int i = 0 ; i < n ; i++)
    {
        dp3[0] = arr[i][0];
        for(int j = 1 ; j < m ; j++)
        {
            dp3[j] = max(dp3[j],dp3[j-1]) + arr[i][j];
        }
    }
    return dp3[m-1];
}

int main()
{
    init();
    cout << fun1() << endl;
    cout << "-----" << endl;
    for(int i = 0 ; i < n ; i++)
    {
        for(int j = 0 ; j < m ; j++)
            cout << dp[i][j] << " ";
        cout << endl;
    }
    cout << endl;
    cout << fun2() << endl;
    cout << "-----" << endl;
    for(int i = 0 ; i < m ; i++)
    {
        cout << dp2[0][i] << " ";
    }
    cout << endl;
    for(int i = 0 ; i < m ; i++)
    {
        cout << dp2[1][i] << " ";
    }
    cout << endl;
    cout << "-----" << endl;
    cout << fun3() << endl;


    return 0;
}