[每日一题]:The Lazy Cow(silver)

题目:

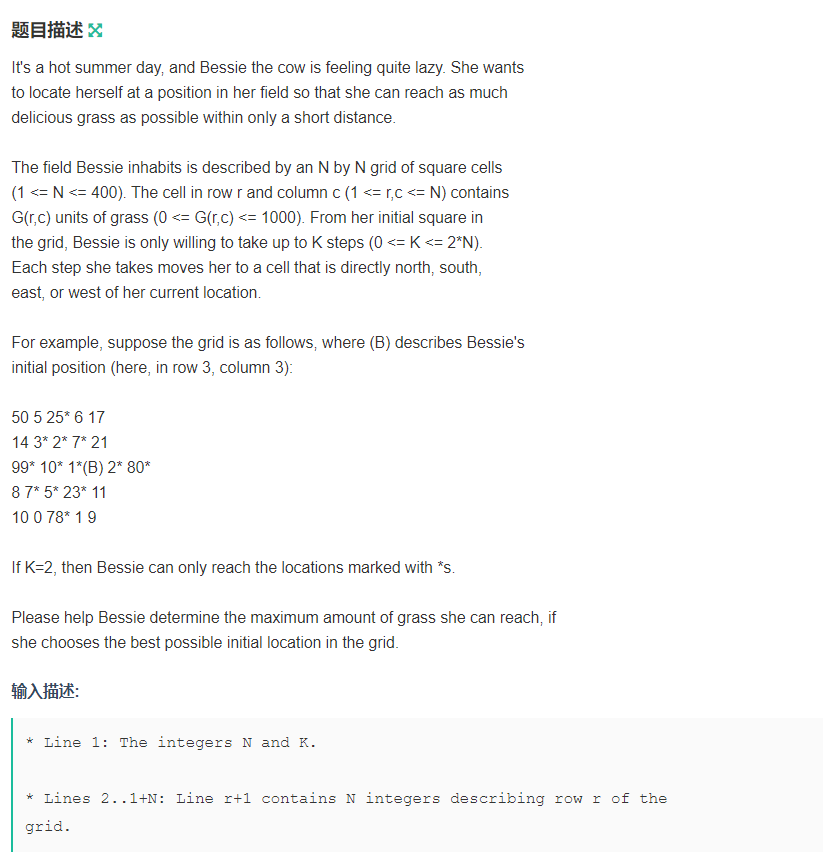
样例:

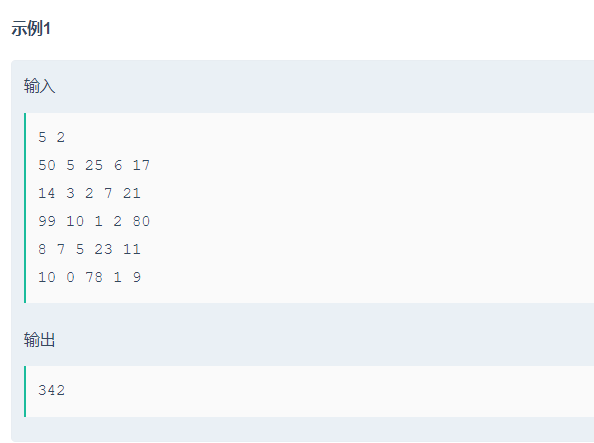
题目大意:

给一个矩阵,然后可以从其中任意一个点走 k 步,每步可以走向 上、下、左、右 4 个方向,求在这个矩阵中走完
k 步后的最大值。
实际上就是求一个正方形中最大的一个区域(这个区域由一个中心点向外扩散,是一个菱形)。

析题得侃:

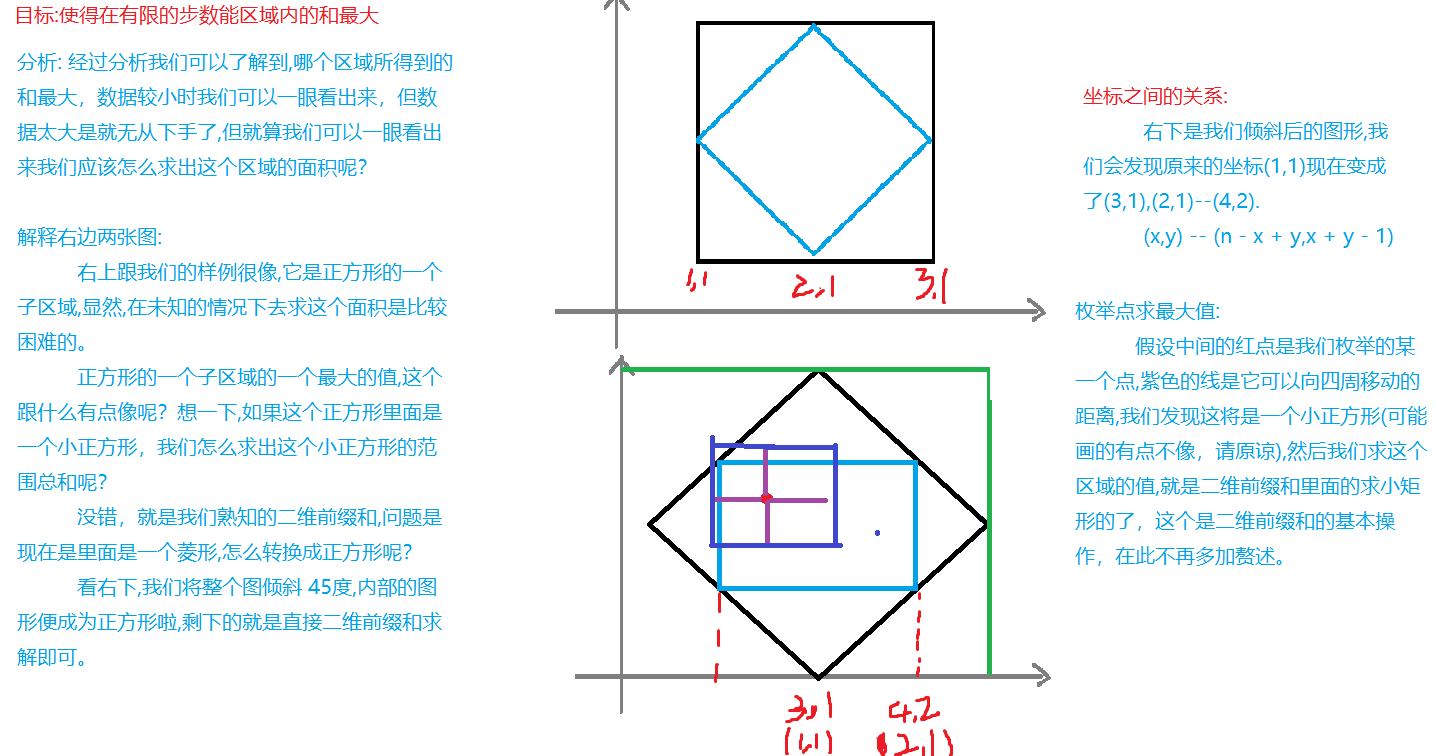
Code:

TLE代码:

#include <queue>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 405;

typedef long long LL;

struct node {
	LL x,y,step;
};

LL a[maxn][maxn],vis[maxn][maxn];
int dir[][2] = {{1,0},{-1,0},{0,1},{0,-1}}; 

LL n,k;

LL res = 0;

LL BFS(int sx,int sy) {
	memset(vis,0,sizeof(vis));
	LL sum = 0;
	queue<node>Q;
	node c,b;
	c.x = sx,c.y = sy;
	c.step = 0;
	Q.push(c);
	while(Q.size()) {
		node top = Q.front();
		Q.pop();
		if(top.step >= k) continue;
		for(int i = 0; i < 4; i ++) {
			int xx = top.x + dir[i][0];
			int yy = top.y + dir[i][1];
			if(xx < 1 || yy < 1 || xx > n || yy > n) continue;
			if(vis[xx][yy]) continue; 
			int step = top.step + 1;
			vis[xx][yy] = 1;
			sum = sum + a[xx][yy];
			Q.push({xx,yy,step});
		}
	}
	return sum;
} 

int main(void) {
	scanf("%lld%lld",&n,&k);
	LL maxValue = -1;
	for(int i = 1; i <= n; i ++) {
		for(int j = 1; j <= n; j ++) {
			scanf("%lld",&a[i][j]);
			res += a[i][j];
			maxValue = max(maxValue,a[i][j]);
		}
	}	
	if(k == 0) cout << maxValue << endl;
	else if(k >= n) printf("%lld
",res);
	else {
		LL ans = -1;
		for(int i = 1; i <= n; i ++) {
			for(int j = 1; j <= n; j ++) {
				ans = max(ans,BFS(i,j));
			}
		}
		printf("%lld
",ans);
	}
	return 0;
} 

AC代码:

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int maxn = 1000;

// B 数组是 A 数组的二倍,倾斜后范围扩大(对应的点有所改变,为了便于计算,遂扩大空间) 
int a[maxn][maxn],b[maxn][maxn],s[maxn][maxn];

int n,k;

int main(void) {
	scanf("%d%d",&n,&k);
	for(int i = 1; i <= n; i ++) {
		for(int j = 1; j <= n; j ++) {
			scanf("%d",&a[i][j]);
		}
	}
	int m = n * 2 - 1;                        // B 数组的范围 
	for(int i = 1; i <= n; i ++) {			  // 倾斜对应的关系(不好找) 
		for(int j = 1; j <= n; j ++) {
			b[n - i + j][i + j - 1] = a[i][j]; 
		}
	}
	LL res = -1;
	for(int i = 1; i <= m; i ++) {			 // 前缀和 
		for(int j = 1; j <= m; j ++) {
			s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + b[i][j];
		}
	}
	LL ans = 0;
	for(int i = 1; i <= n; i ++) {
		for(int j = 1; j <= n; j ++) {
			int x = n - i + j,y = i + j - 1; // 得到倾斜后的坐标 
			int x1 = x - k,x2 = x + k,y1 = y - k,y2 = y + k;	// 对角的坐标 
			if(x1 < 1) x1 = 1;				 // 不能超过已有的区域 
			if(y1 < 1) y1 = 1;
			if(x2 > m) x2 = m;
			if(y2 > m) y2 = m;
			ans = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
			res = max(ans,res);
		}
	}
	printf("%lld
",res);
	return 0;
} 

后记:

前路漫漫,吾辈仍需努力!