Strategic game
| Time Limit: 2000MS | Memory Limit: 10000K | |
| Total Submissions: 7487 | Accepted: 3482 |
Description
Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?
Your program should find the minimum number of soldiers that Bob has to put for a given tree.
For example for the tree:
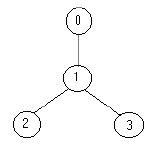
the solution is one soldier ( at the node 1).
Your program should find the minimum number of soldiers that Bob has to put for a given tree.
For example for the tree:

the solution is one soldier ( at the node 1).
Input
The input contains several data sets in text format. Each data set represents a tree with the following description:
The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500);the number_of_roads in each line of input will no more than 10. Every edge appears only once in the input data.
- the number of nodes
- the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifiernumber_of_roads
or
node_identifier:(0)
The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500);the number_of_roads in each line of input will no more than 10. Every edge appears only once in the input data.
Output
The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following:
Sample Input
4 0:(1) 1 1:(2) 2 3 2:(0) 3:(0) 5 3:(3) 1 4 2 1:(1) 0 2:(0) 0:(0) 4:(0)
Sample Output
1 2
没有上司的舞会问题
#include<cstdio> #include<cstring> #include<algorithm> #include<vector> using namespace std; const int MAXN=1505; vector<int> tree[MAXN]; int n; int dp[MAXN][2]; void dfs(int u) { for(int i=0;i<tree[u].size();i++) { int v=tree[u][i]; dfs(v); dp[u][0]+=dp[v][1];//不选自己,则必须选子节点 dp[u][1]+=min(dp[v][1],dp[v][0]);//选上自己,子节点选不选挑个最小的 } dp[u][1]+=1; } int deg[MAXN]; int main() { while(scanf("%d",&n)!=EOF) { memset(dp,0,sizeof(dp)); memset(deg,0,sizeof(deg)); for(int i=0;i<n;i++) tree[i].clear(); for(int i=0;i<n;i++) { int f,m,v; scanf("%d%*c%*c%d%*c",&f,&m); while(m--) { scanf("%d",&v); tree[f].push_back(v); deg[v]++; } } for(int i=0;i<n;i++) { if(deg[i]==0) { dfs(i); printf("%d ",min(dp[i][0],dp[i][1])); break; } } } }