POJ3111(最大化平均值)

K Best

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 8458		Accepted: 2163
Case Time Limit: 2000MS		Special Judge

Description

Demy has n jewels. Each of her jewels has some value v_i and weight w_i.

Since her husband John got broke after recent financial crises, Demy has decided to sell some jewels. She has decided that she would keep k best jewels for herself. She decided to keep such jewels that their specific value is as large as possible. That is, denote the specific value of some set of jewels S = {i₁, i₂, …, i_k} as

.

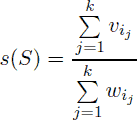Demy would like to select such k jewels that their specific value is maximal possible. Help her to do so.

Input

The first line of the input file contains n — the number of jewels Demy got, and k — the number of jewels she would like to keep (1 ≤ k ≤ n ≤ 100 000).

The following n lines contain two integer numbers each — v_i and w_i (0 ≤ v_i ≤ 10⁶, 1 ≤ w_i ≤ 10⁶, both the sum of all v_i and the sum of all w_i do not exceed 10⁷).

Output

Output k numbers — the numbers of jewels Demy must keep. If there are several solutions, output any one.

Sample Input

3 2
1 1
1 2
1 3

Sample Output

1 2
注意要用G++提交

#include <iostream>
#include <math.h>
#include <algorithm>
using namespace std;
const int MAXN=100005;
const double EPS=1.0e-6;
struct Node{
    int id,v,w;
}a[MAXN];
struct Dou{
    int id;
    double y;
}b[MAXN];
bool comp(const Dou &no1,const Dou &no2)
{
    return no1.y > no2.y;
}
int n,k;
bool test(double x)
{
    for(int i=0;i<n;i++)
    {
        b[i].id=a[i].id;
        b[i].y=a[i].v-x*a[i].w;
    }
    sort(b,b+n,comp);
    double sum=0;
    for(int i=0;i<k;i++)
    {
        sum+=b[i].y;
    }
    return sum>=0.0;
}
int main()
{
    while(cin>>n>>k)
    {
        for(int i=0;i<n;i++)
        {
            a[i].id=i+1;
            cin>>a[i].v>>a[i].w;
        }
        double l=0.0;
        double r=0x3f3f3f3f;
        while(r-l>EPS)
        {
            double mid=(l+r)/2;
            if(test(mid))    l=mid;
            else r=mid;
        }
        for(int i=0;i<k-1;i++)
        {
            cout<<b[i].id<<" ";
        }
        cout<<b[k-1].id<<endl;
    }
    return 0;
}