最近在做信号处理和模式识别的相关技术的研究,有感于介绍这方面的入门文章太少,希望记录些有用的知识帮助需要从事相关工作的朋友少走些弯路。
Matlab大家应该都不陌生,园子里面应该有相当一部分人是学电信或自动控制出身的,我们从事着不同的行业,我们每天写着不同的软件。如果你在做信号处理或者通信相关的行业,相信如果有一天你需要做些原型设计,本文可以引导你快速的开始。
首先让我们来看看matlab的产品定位:
The Language of Technical Computing
MATLAB® is a high-level language and interactive environment that enables
you to perform computationally intensive tasks faster than with traditional
programming languages such as C, C++, and Fortran.
过多的也没必要解释了,就是说一个字“快”,使用matlab可以使你想法更快的被实现出来,做设计的效率是其他编程语言说无法比拟的。据本人所知,数字信号处理里面的滤波器设计,频谱分析,通信中的各种调制技术的设计,matlab可以说已经成了标准工具,就像windows上开发C#代码,大部分人都使用visual studio一样。
首先让我们看看如何产生一些简单有用的序列如何编写:
---注:源代码来自互联网,仅供学习参考之用
function [x,n] = impseq(n0,n1,n2)
% Generates x(n) = delta(n-n0); n1 <= n,n0 <= n2
% ----------------------------------------------
% [x,n] = impseq(n0,n1,n2)
%
if ((n0 < n1) | (n0 > n2) | (n1 > n2))
error('arguments must satisfy n1 <= n0 <= n2')
end
n = [n1:n2];
%x = [zeros(1,(n0-n1)), 1, zeros(1,(n2-n0))];
x = [(n-n0) == 0];
单位阶越:
function [x,n] = stepseq(n0,n1,n2)
再看看如何实现一些简单算法和计算:
序列相加:
% implements y(n) = x1(n)+x2(n)
% -----------------------------
% [y,n] = sigadd(x1,n1,x2,n2)
% y = sum sequence over n, which includes n1 and n2
% x1 = first sequence over n1
% x2 = second sequence over n2 (n2 can be different from n1)
%
n = min(min(n1),min(n2)):max(max(n1),max(n2)); % duration of y(n)
y1 = zeros(1,length(n)); y2 = y1; % initialization
y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; % x1 with duration of y
y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; % x2 with duration of y
y = y1+y2; % sequence addition
序列相乘:
function [y,n] = sigmult(x1,n1,x2,n2)
% -----------------------------
% [y,n] = sigmult(x1,n1,x2,n2)
% y = product sequence over n, which includes n1 and n2
% x1 = first sequence over n1
% x2 = second sequence over n2 (n2 can be different from n1)
%
n = min(min(n1),min(n2)):max(max(n1),max(n2)); % duration of y(n)
y1 = zeros(1,length(n)); y2 = y1; %
y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; % x1 with duration of y
y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; % x2 with duration of y
y = y1 .* y2; % sequence multiplication
LMS算法实现:
% LMS Algorithm for Coefficient Adjustment
% ----------------------------------------
% [h,y] = lms(x,d,delta,N)
% h = estimated FIR filter
% y = output array y(n)
% x = input array x(n)
% d = desired array d(n), length must be same as x
% delta = step size
% N = length of the FIR filter
%
M = length(x); y = zeros(1,M);
h = zeros(1,N);
for n = N:M
x1 = x(n:-1:n-N+1);
y = h * x1';
e = d(n) - y;
h = h + delta*e*x1;
end
DFT算法实现:
function [Xk] = dft(xn,N)
% -----------------------------------
% [Xk] = dft(xn,N)
% Xk = DFT coeff. array over 0 <= k <= N-1
% xn = N-point finite-duration sequence
% N = Length of DFT
%
n = [0:1:N-1]; % row vector for n
k = [0:1:N-1]; % row vecor for k
WN = exp(-j*2*pi/N); % Wn factor
nk = n'*k; % creates a N by N matrix of nk values
WNnk = WN .^ nk; % DFT matrix
Xk = xn * WNnk; % row vector for DFT coefficients
简单序列计算:
2. x(n) = n[u(n)-u(n-10)]+10*exp(-0.3(n-10))(u(n-10)-u(n-20)); 0<=n<=20
3. x(n) = cos(0.04*pi*n) + 0.2*w(n); 0<=n<=50, w(n): Gaussian (0,1)
4. x(n) = {...,5,4,3,2,1,5,4,3,2,1,...}; -10<=n<=9
结果如下:
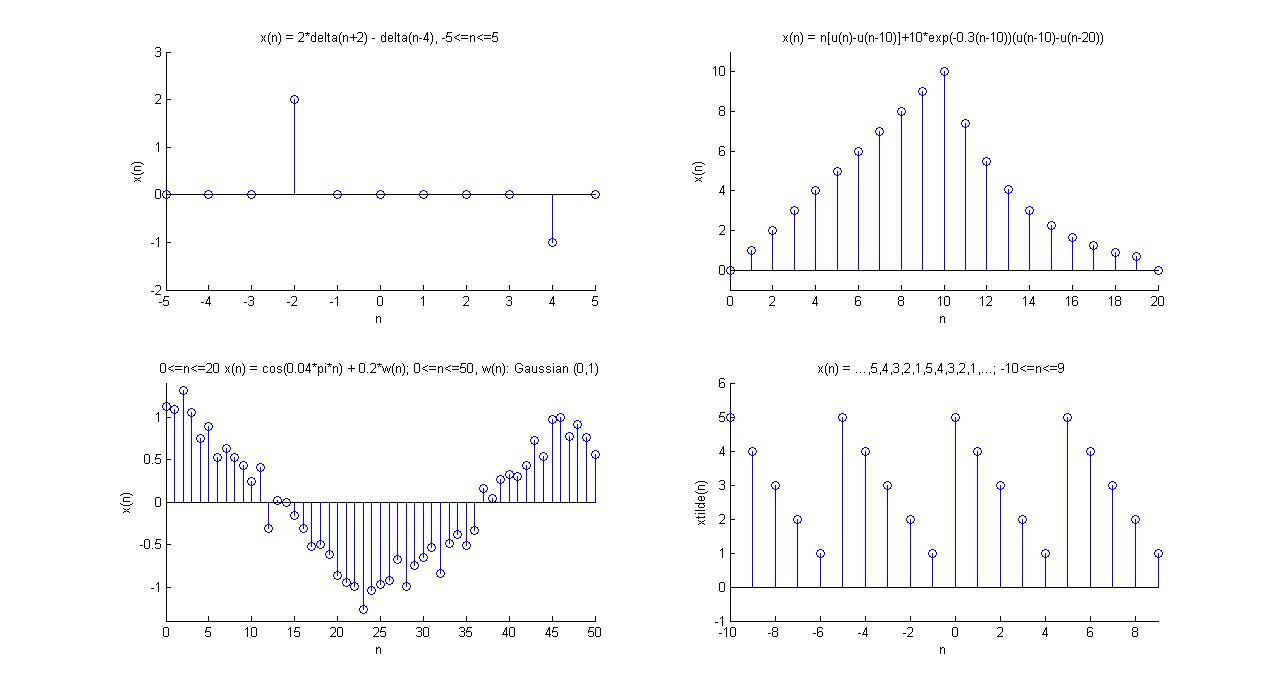
几个简单的语句就可以完成相当复杂的计算,如果用C语言写这中算法,相信设计效率的差距是不言而喻的,工欲善其事必先利其器,选对工具对于做正确的事情是很重要的。
关于学习资料和文档:
推荐matlab的官方手册和help文档,对于每个工具箱的描述和基本功能的介绍都非常的明确,当然资料都是英文的,中文手册我也一直没有找到,如果有朋友有中文的手册,请通知我。
关于书籍,我在书店随便翻看了几本,大部分都是手册翻译,而且都是就某个工具箱的翻译,不是很全,书名倒是都很霸气,如果那个朋友发现好的书籍也请您通知我,我会更新博文,让更多的人受益。
总结:
本文资料源自本人的读书笔记和互联网,通过一些简单的算法和源代码说明了如何用matlab解决相关的问题,当然本文面向的是初学者,如果哪位对高级的topic感兴趣,可以联系我,希望对大家有所帮助。