二项堆其实就是由多棵二项树构成的森林,每棵树的根结点构成一个单链表。其链表序列,按照每棵二项树的度从小到大排列。
依然分析它的五种基本操作:
- make_heap:建立一个空堆,或者把数组中元素转换成二叉堆。
- insert:插入元素。
- minimun:返回一个最小数。
- extract_min:移除最小结点。
- union:合并堆
二项树
说说二项树。
定义
- 二项树B0由一个结点组成。
- 二项树Bk是由两棵二项树Bk-1组成,其中一棵树作为另一颗树的左儿子。
性质
- 二项树Bk具有2k个结点。
- 二项树Bk高度为k。
- 二项树Bk在深度i处有Cki个结点。
- 根的度数为k。
图为一颗B3:
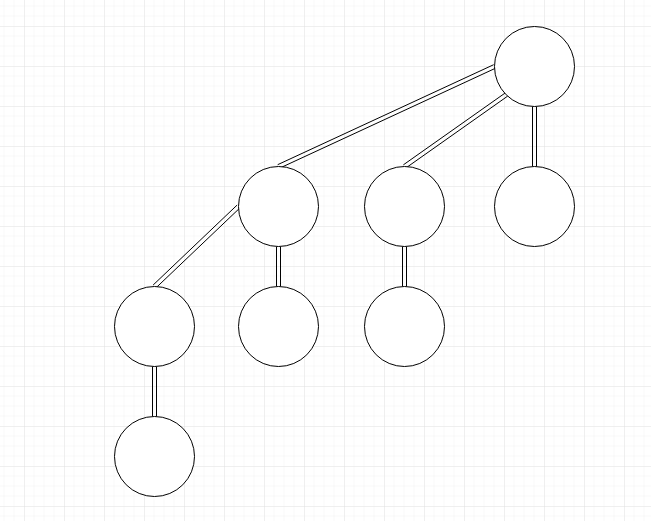
二项堆
说说二项堆,二项堆作为一个二项树的集合,按照根结点的度数大小从小到大排列,每棵二项树都满足堆的性质(以下以最小堆性质为例),同时二项堆里不能有两棵或以上具有相同度数的二项树。
形如: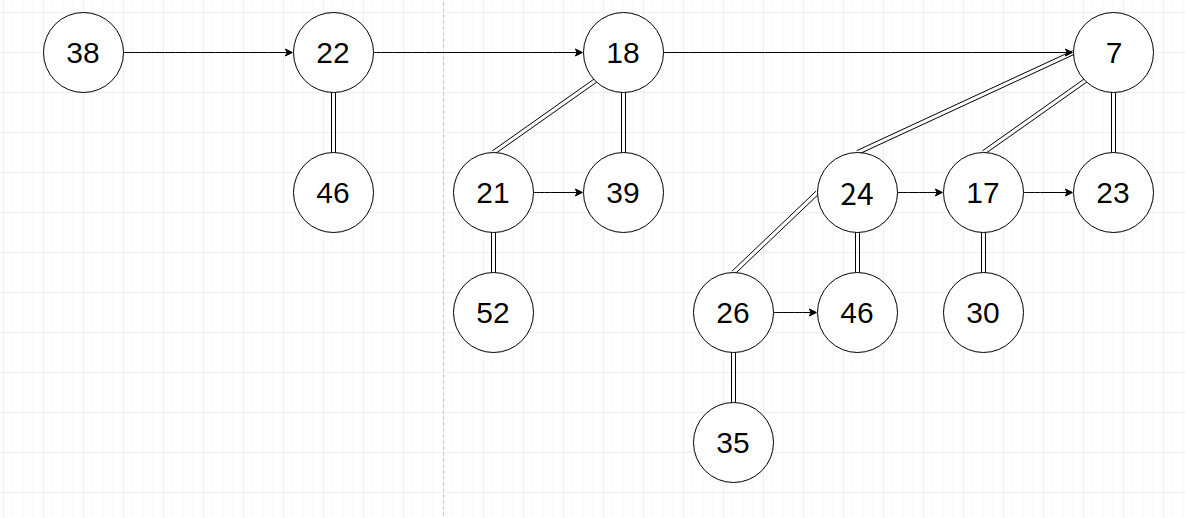
对每个结点做如下定义:
1 typedef struct node { 2 int key;//键值 3 int degree;//度数 4 node *child;//第一个儿子 5 node *parent;//父结点 6 node *next;//兄弟结点 7 } bnode, *bheap;
基本操作
make_heap
建立新堆只需要分配一个二项堆的结点。生成一个堆对象便可。所以时间复杂度为O(1)。
1 bnode *Make_Node(int key) { 2 bnode *node; 3 node = new bnode; 4 node->key = key; 5 node->degree = 0; 6 node->parent = nullptr; 7 node->child = nullptr; 8 node->next = nullptr; 9 return node; 10 }
union
合并两个二项堆。时间复杂度为O(logn)
- 将两个堆的根节点链表按照二项树度数从小到大重新组合。
- 然后从左至右开始将相同度数的二项树合并,合并分为四种情况。
- 当前结点和下一结点的度数不等时,不进行操作向后观察。
- 当前结点、下一结点和下二结点度数都相等,暂时不进行处理,继续向后观察,这是为了从最后的两个相同度数的树处理。
- 当前结点度数与下一结点度数相等、下一结点度数与下二结点度数不等的时候,并且当前结点的键值小于等于下一结点的键值,此时,将下一结点作为当前结点的第一个儿子。
- 当前结点度数与下一结点度数相等、下一结点度数与下二结点度数不等的时候,并且当前结点的键值大于下一结点的键值,此时,将当前结点作为下一结点的第一个儿子。
图示
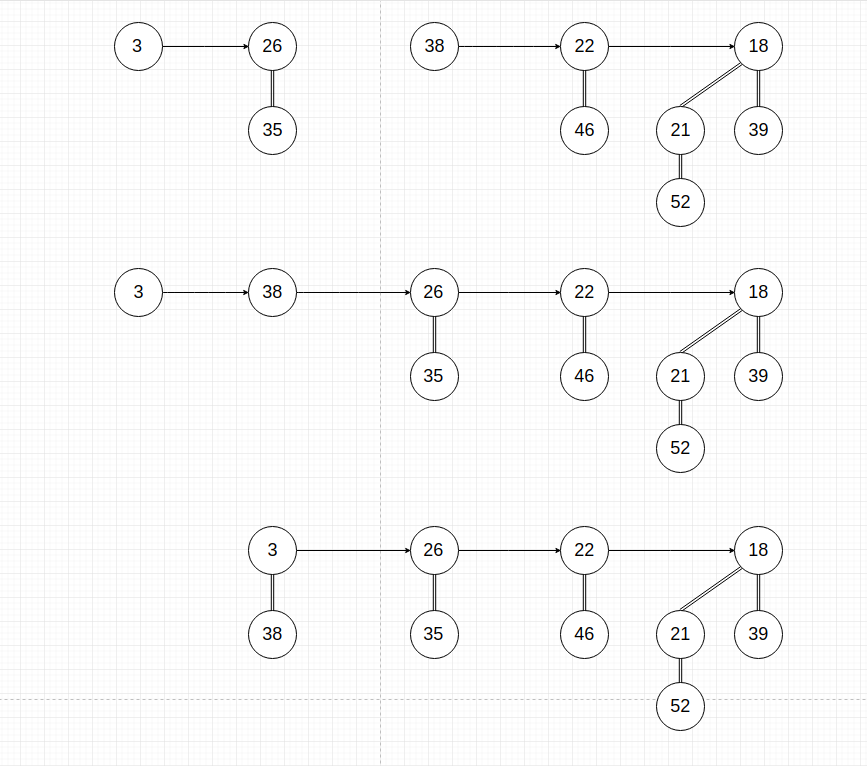
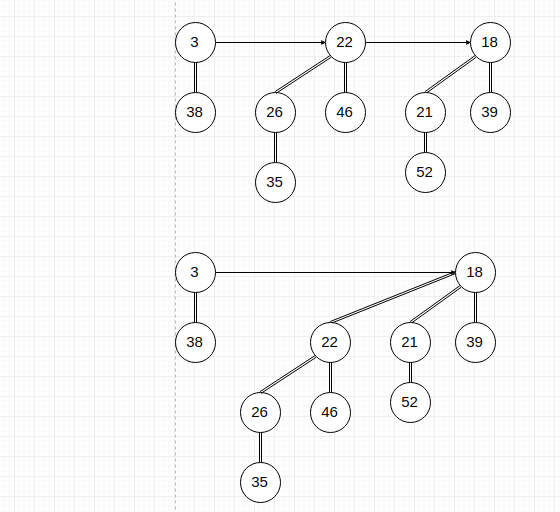
代码实现
1 //合并两个根节点链表 2 bnode *Merge(bheap h1, bheap h2) { 3 if (h1 == nullptr) return h2; 4 else if (h2 == nullptr) return h1; 5 bnode *head = nullptr; 6 if (h1->degree < h2->degree) { 7 head = h1; 8 head->next = Merge(h1->next, h2); 9 } else { 10 head = h2; 11 head->next = Merge(h2->next, h1); 12 } 13 return head; 14 } 15 16 //将两个相邻的根树合并 17 void Link(bheap child, bheap heap) { 18 child->parent = heap; 19 child->next = heap->child; 20 heap->child = child; 21 heap->degree++; 22 } 23 24 //合并 25 bnode *Union(bheap h1, bheap h2) { 26 bnode *heap; 27 bnode *pre_x, *x, *nxt_x; 28 heap = Merge(h1, h2); 29 if (heap == nullptr) return nullptr; 30 pre_x = nullptr; 31 x = heap; 32 nxt_x = x->next; 33 while (nxt_x != nullptr) { 34 if ((x->degree != nxt_x->degree) 35 || ((nxt_x->next != nullptr) 36 && (nxt_x->degree == nxt_x->next->degree))) { 37 pre_x = x; 38 x = nxt_x; 39 } else if (x->key <= nxt_x->key) { 40 x->next = nxt_x->next; 41 nxt_x->parent = x; 42 Link(nxt_x, x); 43 } else { 44 if (pre_x == nullptr) heap = nxt_x; 45 else pre_x->next = nxt_x; 46 Link(x, nxt_x); 47 x = nxt_x; 48 } 49 nxt_x = x->next; 50 } 51 return heap; 52 }
insert
有了合并操作,插入操作也就很好实现了,只需要将新加入的结点与原二项堆合并即可。时间复杂度等同于union,为O(logn)
代码实现
1 bnode *Insert(bheap heap, int key) { 2 bnode *node; 3 node = Make_Node(key); 4 if (node == nullptr) return heap; 5 return Union(heap, node); 6 }
minimun
对于二项堆,其最小结点必然在根链表中,所以只要遍历一遍根链表就可以找到。根链表由logn个结点组成,所以时间复杂度为O(logn),如果在其他操作中设置一个指针反复更新最小结点位置,那么时间复杂度可以压缩至O(1)。
代码实现
1 bnode *Minimun(bheap heap) { 2 bnode *pos = heap; 3 bnode *minn = heap; 4 while (pos != nullptr) { 5 if (pos->key < minn->key) minn = pos; 6 pos = pos->next; 7 } 8 return minn; 9 }
extract_min
移除最小结点,因为最小结点必然在根链表中,所以此操作可以:
- 将最小根结点的二项树从原二项堆中移除。
- 将此二项树根结点删除。
- 将此根结点的儿子链表作为新的根链表构成新的二项堆。注意二项堆中二项树需按照度数从小到大排列。
- 然后将这个二项堆与原二项堆合并。
时间复杂度O(logn)。
图示

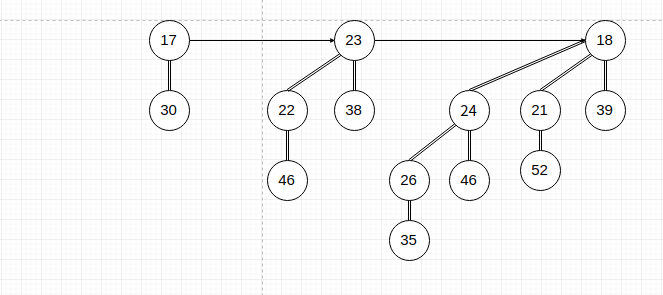
代码实现
1 //将子树们转换成一个新的二项堆 2 bnode *Transform(bheap heap) { 3 bnode *next; 4 bnode *tail = nullptr; 5 if (!heap) return heap; 6 heap->parent = nullptr; 7 while (heap->next) { 8 next = heap->next; 9 heap->next = tail; 10 tail = heap; 11 heap = next; 12 heap->parent = nullptr; 13 } 14 heap->next = tail; 15 return heap; 16 } 17 18 //删除最小堆顶元素 19 bnode *Extract_Min(bheap heap) { 20 bnode *minnode = Minimun(heap); 21 bnode *pre, *pos; 22 pre = nullptr; 23 pos = heap; 24 while (pos != minnode) { 25 pre = pos; 26 pos = pos->next; 27 } 28 if (pre) pre->next = minnode->next; 29 else heap = minnode->next; 30 heap = Union(heap, Transform(minnode->child)); 31 delete (minnode); 32 return heap; 33 }
最后一想,二项堆其实也就在合并上比之二叉堆来的优秀。但是在二项堆相似的思想上可以继续优化,下一篇再随便说说斐波那契堆。