模型介绍
对于分类问题,其得到的结果值是离散的,所以通常情况下,不适合使用线性回归方法进行模拟。
所以提出Logistic回归模型。
其假设函数如下:
[h_θ(x)=g(θ^Tx)
]
函数g定义如下:
[g(z)=frac{1}{1+e^{-z}}(z∈R)
]
所以假设函数书写如下:
[h_θ(x)=frac{1}{1+e^{-θ^Tx}}
]
图像类似如下:
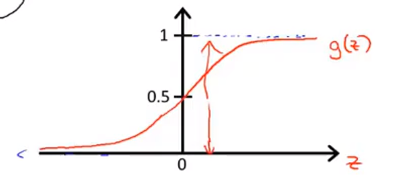
根据图像我们可以看出,当g(z)中的z大于0的时候,其g(z)则大于0.5,则此状态下的可能性则更大。
决策边界
对于假设函数hθ,当确定了其中所有的系数θ,则可以将(θ^Tx)绘制出一个用于区分结果值0与1之间的边界。
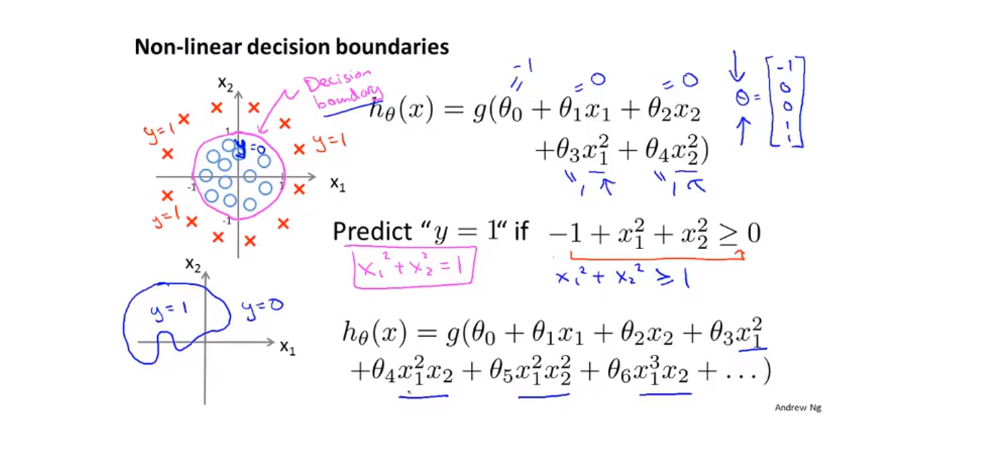
代价函数
和线性回归相同,代价函数可以用于构造最合适的系数θ。
[J(θ)=frac{1}{m}sum_{i=1}^{m}{cost(h_θ(x)-y)}
]
[cost(h_θ(x)-y)=egin{cases}
-log(h_θ(x)) & if & y=1 \
-log(1-h_θ(x)) & if & y=0
end{cases}
]
[J(θ)=frac{1}{m}[sum_{i=1}^{m}{y^{(i)}logh_θ(x^{(i)})+(1-y^{(i)})log(1-h_θ(x^{(i)}))}]
]

分析
对于cost函数,在y=1的时候,很明显当(h_θ(x))趋近于1的时候,cost函数接近于0,则代价函数(J(θ))也接近于0,合理;(h_θ(x))趋近于0的时候,cost函数趋近于无穷大,而代价函数(J(θ))也趋于无穷大,这是不合理的。从代价函数本身的意义出发,就是寻找当代价函数(J(θ))最小的时候,就得到最合理的系数θ。
梯度下降
为了获得最小的(J(θ))
给出:
[θ_j:=θ_j-αfrac{∂}{∂θ_j}J(θ)
]
[θ_j:=θ_j-αfrac{1}{m}sum_{i=1}^{m} {(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}}
]
通过不断迭代得到最终合适的θ。
一对多问题
对于很多分类问题,不只是需要分类为两类0,1,可能需要做更多的分类。
对于解决这类问题可以采用回归分类器,见下图:
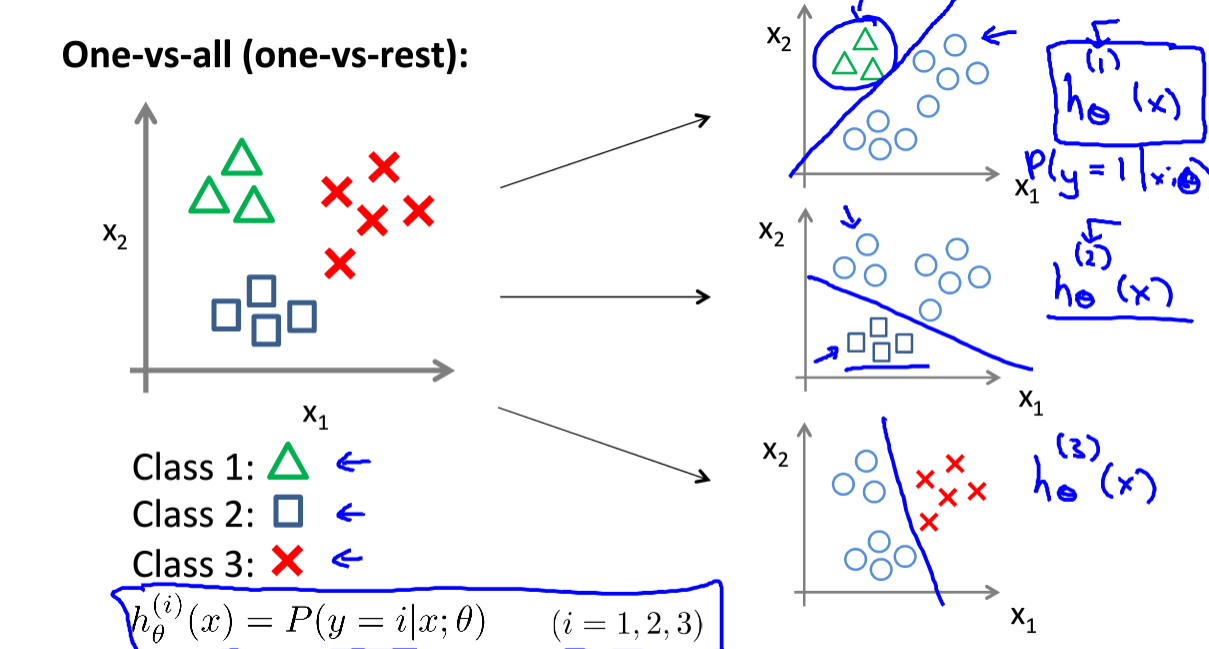
对于多个分类,可以选择将需要判断的那个分类定义为正类,其余都定义为负类,执行logistic回归得到一个假设函数(h_θ^{(i)}),使用时,选择最为合适的假设函数进行模拟即可。