for (var i=0;i<10;i++){ console.log(Math.random().toFixed(2)*100) }
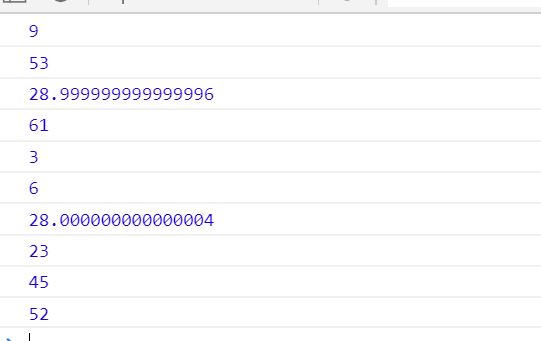
这个代码中利用随机取数选取 两位小数去乘以100
我们可以看到有两个出现了误差
其实对于浮点数的四则运算,几乎所有的编程语言都会有类似精度误差的问题,只不过在 C++/C#/Java 这些语言中已经封装好了方法来避免精度的问题,而 JavaScript 是一门弱类型的语言,从设计思想上就没有对浮点数有个严格的数据类型,所以精度误差的问题就显得格外突出。下面就分析下为什么会有这个精度误差,以及怎样修复这个误差。
首先,我们要站在计算机的角度思考 0.1 + 0.2 这个看似小儿科的问题。我们知道,能被计算机读懂的是二进制,而不是十进制,所以我们先把 0.1 和 0.2 转换成二进制看看:
0.1 => 0.0001 1001 1001 1001…(无限循环)
0.2 => 0.0011 0011 0011 0011…(无限循环)
上面我们发现0.1和0.2转化为二进制之后,变成了一个无限循环的数字,这在现实生活中,无限循环我们可以理解,但计算机是不允许无限循环的,对于无限循环的小数,计算机会进行舍入处理。进行双精度浮点数的小数部分最多支持 52 位,所以两者相加之后得到这么一串 0.0100110011001100110011001100110011001100110011001100 因浮点数小数位的限制而截断的二进制数字,这时候,我们再把它转换为十进制,就成了 0.30000000000000004。
知道了浮点数产生的原因了,那么怎么处理这个问题呢?
方法一:指定要保留的小数位数(0.1+0.2).toFixed(1) = 0.3;这个方法toFixed是进行四舍五入的也不是很精准,对于计算金额这种严谨的问题,不推荐使用,而且不同浏览器对toFixed的计算结果也存在差异。
方法二:把需要计算的数字升级(乘以10的n次幂)成计算机能够精确识别的整数,等计算完毕再降级(除以10的n次幂),这是大部分编程语言处理精度差异的通用方法。
网上的处理方法:
//加法 Number.prototype.add = function(arg){ var r1,r2,m; try{r1=this.toString().split(".")[1].length}catch(e){r1=0} try{r2=arg.toString().split(".")[1].length}catch(e){r2=0} m=Math.pow(10,Math.max(r1,r2)) return (this*m+arg*m)/m } //减法 Number.prototype.sub = function (arg){ return this.add(-arg); } //乘法 Number.prototype.mul = function (arg) { var m=0,s1=this.toString(),s2=arg.toString(); try{m+=s1.split(".")[1].length}catch(e){} try{m+=s2.split(".")[1].length}catch(e){} return Number(s1.replace(".",""))*Number(s2.replace(".",""))/Math.pow(10,m) } //除法 Number.prototype.div = function (arg){ var t1=0,t2=0,r1,r2; try{t1=this.toString().split(".")[1].length}catch(e){} try{t2=arg.toString().split(".")[1].length}catch(e){} with(Math){ r1=Number(this.toString().replace(".","")) r2=Number(arg.toString().replace(".","")) return (r1/r2)*pow(10,t2-t1); } }* ** method **
* add / subtract / multiply /divide * * ** explame ** * 0.1 + 0.2 == 0.30000000000000004 (多了 0.00000000000004) * 0.2 + 0.4 == 0.6000000000000001 (多了 0.0000000000001) * 19.9 * 100 == 1989.9999999999998 (少了 0.0000000000002) * * floatObj.add(0.1, 0.2) >> 0.3 * floatObj.multiply(19.9, 100) >> 1990 * */var floatObj = function() { /* * 判断obj是否为一个整数 */ function isInteger(obj) { return Math.floor(obj) === obj } /* * 将一个浮点数转成整数,返回整数和倍数。如 3.14 >> 314,倍数是 100 * @param floatNum {number} 小数 * @return {object} * {times:100, num: 314} */ function toInteger(floatNum) { var ret = {times: 1, num: 0} if (isInteger(floatNum)) { ret.num = floatNum return ret } var strfi = floatNum + '' var dotPos = strfi.indexOf('.') var len = strfi.substr(dotPos+1).length var times = Math.pow(10, len) var intNum = parseInt(floatNum * times + 0.5, 10) ret.times = times ret.num = intNum return ret } /* * 核心方法,实现加减乘除运算,确保不丢失精度 * 思路:把小数放大为整数(乘),进行算术运算,再缩小为小数(除) * * @param a {number} 运算数1 * @param b {number} 运算数2 * @param digits {number} 精度,保留的小数点数,比如 2, 即保留为两位小数 * @param op {string} 运算类型,有加减乘除(add/subtract/multiply/divide) * */ function operation(a, b, digits, op) { var o1 = toInteger(a) var o2 = toInteger(b) var n1 = o1.num var n2 = o2.num var t1 = o1.times var t2 = o2.times var max = t1 > t2 ? t1 : t2 var result = null switch (op) { case 'add': if (t1 === t2) { // 两个小数位数相同 result = n1 + n2 } else if (t1 > t2) { // o1 小数位 大于 o2 result = n1 + n2 * (t1 / t2) } else { // o1 小数位 小于 o2 result = n1 * (t2 / t1) + n2 } return result / max case 'subtract': if (t1 === t2) { result = n1 - n2 } else if (t1 > t2) { result = n1 - n2 * (t1 / t2) } else { result = n1 * (t2 / t1) - n2 } return result / max case 'multiply': result = (n1 * n2) / (t1 * t2) return result case 'divide': result = (n1 / n2) * (t2 / t1) return result } } // 加减乘除的四个接口 function add(a, b, digits) { return operation(a, b, digits, 'add') } function subtract(a, b, digits) { return operation(a, b, digits, 'subtract') } function multiply(a, b, digits) { return operation(a, b, digits, 'multiply') } function divide(a, b, digits) { return operation(a, b, digits, 'divide') } // exports return { add: add, subtract: subtract, multiply: multiply, divide: divide }}();toFixed的修复如下// toFixed 修复function toFixed(num, s) { var times = Math.pow(10, s) var des = num * times + 0.5 des = parseInt(des, 10) / times return des + ''}