//hdu1086 求n个线段相交点数量。。.
//http://acm.hdu.edu.cn/showproblem.php?pid=1086
//以下为翻译后的tip:
//给您N(1 <= N <= 100)个细分(线段),请输出所有交叉点的数量。如果M(M> 2)个线段在同一点相交,则应重复计算。
//您可以假设两个线段相交的点不会超过一个。(不重合)
// 解法很一般:遍历每两条线段,判断是否有交点。
//判断两直线是否相交的办法:(先求直线的交点)两直线联立。求交点坐标。。。//然后判断交点在不在这两条线段上
// 高中知识,不要记忆,直接推导即可。
//直线一般式方程:(y2 - y1) * x + (x1 - x2) * y + (x2 * y1 - x1 * y2) = 0; 原式(A*x + B*y + C = 0)
//交点坐标 x: (b1 * c2 - b2 * c1) / (a1 * b2 - a2 * b1) , y: (a2 * c1 - a1 * c2) / (a1 * b2 - a2 * b1);
//如果 a1 * b2 - a2 * b1 == 0 则表示(直线)没有交点(平行)
1 #include<cstdio> 2 3 struct Line { 4 double x1, y1, x2, y2; 5 } line[105]; 6 7 int n; 8 9 bool intersect(int l1, int l2) { 10 double a1 = line[l1].y2 - line[l1].y1; 11 double b1 = line[l1].x1 - line[l1].x2; 12 double c1 = line[l1].x2*line[l1].y1 - line[l1].x1*line[l1].y2; 13 double a2 = line[l2].y2 - line[l2].y1; 14 double b2 = line[l2].x1 - line[l2].x2; 15 double c2 = line[l2].x2*line[l2].y1 - line[l2].x1*line[l2].y2; 16 if(a1*b2 - a2*b1 == 0) return false; 17 double x = (b1*c2 - b2*c1)/(a1*b2 - a2*b1); 18 double y = (a2*c1 - a1*c2)/(a1*b2 - a2*b1); 19 if((x >= line[l1].x1 && x <= line[l1].x2 || x <= line[l1].x1 && x >= line[l1].x2) 20 && (x >= line[l2].x1 && x <= line[l2].x2 || x <= line[l2].x1 && x >= line[l2].x2)) return true; 21 return false; 22 } 23 24 int main() { 25 while(scanf("%d", &n) == 1 && n) { 26 for(int i = 0; i != n; ++i) { 27 scanf("%lf%lf%lf%lf", &line[i].x1, &line[i].y1, &line[i].x2, &line[i].y2); 28 } 29 int ans = 0; 30 for(int i = 0; i != n-1; ++i) { 31 for(int j = i+1; j != n; ++j) { 32 if(intersect(i, j)) ans++; 33 } 34 } 35 printf("%d ", ans); 36 } 37 return 0; 38 }
//————————————————————分割————
//hdu 1071 定积分的简单题
http://acm.hdu.edu.cn/showproblem.php?pid=1071
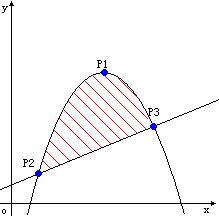
//后悔当初没有好好学高数。。。
//一元二次方程顶点式:y = a(x - h) ^ 2 +k 顶点 p (h, k);
//直线方程 y = kx + b
//y1 为抛物线方程 y2为直线方程 求 积分f(y1 - y2)[x1~x2];
1 #include<cstdio> 2 3 int main() { 4 int T; 5 scanf("%d", &T); 6 while(T--) { 7 double p1x, p1y, p2x, p2y, p3x, p3y; 8 scanf("%lf%lf%lf%lf%lf%lf", &p1x, &p1y, &p2x, &p2y, &p3x, &p3y); 9 double a = (p2y-p1y)/((p2x-p1x)*(p2x-p1x));//(二次方程中的a) 10 double k = (p3y-p2y)/(p3x-p2x);//(直线斜率) 11 double b = p2y-k*p2x;//(截距) 12 double s1 = a*p2x*p2x*p2x/3.0 - (2*a*p1x+k)*p2x*p2x/2.0 + (a*p1x*p1x+p1y-b)*p2x; 13 double s2 = a*p3x*p3x*p3x/3.0 - (2*a*p1x+k)*p3x*p3x/2.0 + (a*p1x*p1x+p1y-b)*p3x; 14 if(s1 - s2 > 0) printf("%.2lf ", s1-s2); 15 else printf("%.2lf ", s2-s1); 16 } 17 return 0; 18 }