洛谷 P1011 车站

　　提供两种解法，第一种解法利用递推公式（借鉴dingcx的代码），第二种解法则是利用枚举依次列举出来，如果符合条件的话便输出答案

1.递推：根据题意可列出一个表格

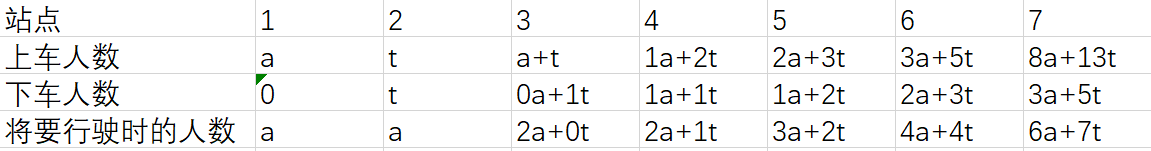
由于第2站上车的人数是未知的，暂且将其设成 t，那么由表格可得出相应的规律，如第一行和第二行从某一列开始，a 和 t 的系数便是前面两项的相加之和，

相应的，我们猜测第三行也具有类似的规律，观察发现从第四列开始，a 和 t 的系数分别为前两个表达式中a系数的和 -1 和t系数的和 +1，因此便可以得出在某一站点时的人数，

设 a 和 t 的值为 index1[ i ]和index2[ i ]

index1[i]= index1[i-1] + intex1[i-2]-1;//前两个的和-1

index2[i]= index2[i-1] + index2[i-2]+1; //和+1

在这之后，t的值也能算出来了，由于m=a* index1[n-1]+b* index2[n-1]=a∗ index1[n−1]+b∗ index2[n−1]

所以 b = (m - a*index1[n - 1]) / index2[n - 1];

由于最后一站（ 第 n 站）不会有人上车，车上的人都下去，那么第n站的人数也就是第n - 1站出发时车上的人数。

下面是代码：

#include <stdio.h>
int index1[21]index2[21];
int a, n, m, x;
int main(){
    scanf("%d %d %d %d",&a,&n,&m,&x);
    index[2] = 1;
    index[3] = 2;
    for(int i = 4; i <= n; i ++){
        index[i] = index[i - 1] + index[i - 2] - 1;
        index[i] = index[i - 1] +index[i - 2] + 1;
    }
    int b = (m - a*index1[n - 1]) / index2[n - 1];
    printf("%d
",a*index1[x] + b*index2[x]);
    return 0;
}

第二种利用枚举法：

从第2站开始，设其上车和下车的人数都是num,则从前往后由0开始枚举，当到最后一站时车上人数和m相等便符合题意。

#include <stdio.h>
int up[1000],down[1000],last[1000];
int a, n, m, x;
int main(){
    scanf("%d %d %d %d",&a,&n,&m,&x);
    up[1] = a;
    down[1] = a;
    for(int i = 0; ; i ++){
        up[2] = i;
        last[2] = i;
        for(int j = 3;j <= n - 1; j ++){
            up[j] = up[j - 1] + up [j - 2];
            down[j] = up[j - 1];
            last[j] = last[j - 1] + up[j] - down[j];
        }
        if(last[i] == m){
            printf("%d
",last[x]);
            break;
        }
    }
    return 0;
}