【算法】动态规划经典题之最长公共子序列

动态规划经典题之最长公共子序列

参考：最长公共子序列与最长公共子串

概念

最长公共子序列： 两个字符串中相同的子串序列，可以不连续。

最长公共子串： 两个字符串中相同的连续子串。

这两者的区别就在于子串是否需要连续。

状态转移方程

最长公共子串：

我们记c[i, j]为x和y在长度为i和j时的最长公共子序列的长度，当x或y的长度为0时，c[i, j]必定为0。当x长度为i，y长度为j时，如果xi == yj，则根据之前计算的结果向前退一位，c[i, j] = c[i-1, j-1] + 1，否则c[i, j] = 0。这是由于连续性导致的。

最长公共子序列：

同理我们推导最长公共子序列的状态转移方程，i=0或j=0时跟最长公共子串是一样的，但是在i,j>0且xi != yj时，c[i,j]并不是简单的等于0，而是将i或j向前退一位，取c[i-1, j]和c[i, j-1]之间的最大值，这是因为最长公共子序列是可以不连续的。

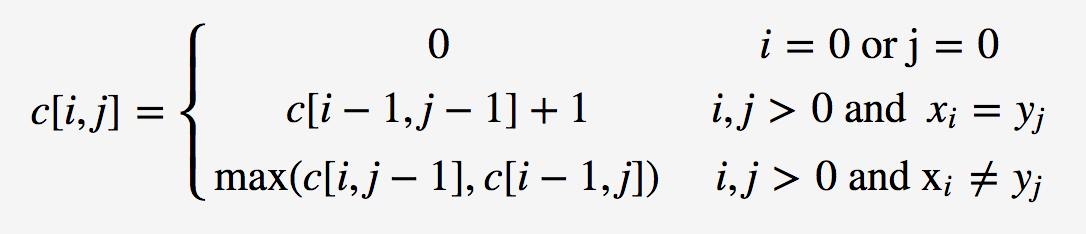
代码

最长公共子串：

/**
 * 最长公共子串
 * @param s source string
 * @param t target string
 * @return 最长公共子串的长度
 */
public static int lcs1(String s, String t) {
    if (s == null || s.length() == 0 || t == null || t.length() == 0) return 0;

    int len1 = s.length(), len2 = t.length();

    int[][] dp = new int[len1+1][len2+1];

    int max = 0;

    for (int i = 0; i <= len1; i++) {
        for (int j = 0; j <= len2; j++) {
            //处理i=0和j=0的情况，自底向上进行初始化
            if (i == 0 || j == 0) dp[i][j] = 0;
            else if (s.charAt(i-1) == t.charAt(j-1)) {
                dp[i][j] = dp[i-1][j-1] + 1;
            }else {
                dp[i][j] = 0;
            }

            if (max < dp[i][j])
                max = dp[i][j];
        }
    }

    return max;
}

最长公共子序列：

/**
 * 最长公共子序列
 * @param s source string
 * @param t target string
 * @return 最长公共子序列的长度
 */
public static int lcs(String s, String t) {
    if (s == null || s.length() == 0 || t == null || t.length() == 0) return 0;

    int len1 = s.length(), len2 = t.length();

    int[][] dp = new int[len1+1][len2+1];

    int max = 0;

    for (int i = 0; i <= len1; i++) {
        for (int j = 0; j <= len2; j++) {
            if (i == 0 || j == 0) dp[i][j] = 0;
            else if (s.charAt(i-1) == t.charAt(j-1)) {
                dp[i][j] = dp[i-1][j-1] + 1;
            }else {
            	//和最长公共子串不一样的地方
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
            }

            if (max < dp[i][j])
                max = dp[i][j];
        }
    }

    return max;
}