首先,解决一个数学问题,需要有一定的基础知识。
基础知识又分为:1. 安全变换 ;2. 启发式变换;3. 基本变换公式
其次,要程序化的解决一个数学问题,需要建立目标树:
*所谓树,到达最终的“解决果实”,可能有分叉,也就是说,可以若干条分支,最终摘到果实。
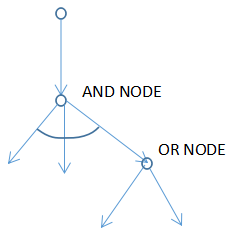
AND NODE:就是必须将问题全部解决的节点
OR NODE:就是可以选择一条支解决,如果一条支解决不了,可以回到节点处选择另一条支。
例子:解 ∫ - ( 5 *( ( X )4 / ( ( 1 - (X)2 ) )5 / 2 )) dx *此公式其实没便要那么多括号,但为了方便程序化的优先级
准备知识:
一. 安全变换
1. ∫ -f(x) dx = - ∫ f(x) dx
2. ∫ C* f(x) dx = C * ∫ f(x) dx
3. ∫ Σ fi(x) dx = Σ ∫ fi(x) dx
4. ∫ (f(x) / g(x) )dx = f (q(x) + 1 / g(x) ) dx
……
*安全变换,其实有十多种,这是常用的几种
二. 启发变换
5. ∫ f(tan(x)) dx = ∫ f(y) / (1 + (y)2) dy
6. 若存在 1 - (x)2,那么令 x = sin(y);若存在1 + (x)2,那么令 x = tan(y)
……
*启发变换,其实有十多种,这是常用的几种
三. 基本变换公式:积分表
OK,然后开始解决:
1. 根据安全变换1,问题变为,解决:∫ 5 * (( X )4 ) / ( ( 1 - (X)2 ) )5 / 2) dx
2. 根据安全变换2,问题变为,解决:∫ ( X )4 / ( ( 1 - (X)2 ) )5 / 2dx
3. 现在,有一个OR NODE,使用安全变换4,OR,使用启发变换。
3.1
先使用启发变换:
令:x = sin(y) , dx / dy = cos(y) ,dx = cos(y) dy, 1 - X2 = 1 - (sin(y))2 = cos(y)2
4. 问题变为,解决:∫ (sin(y))4 / (cos(y))4 dy
3.2
……
3.1.1
现在,有一个OR NODE,∫ (sin(y))4 / (cos(y))4 dy 变为: ∫ 1 / (cot(y))4 dy OR ∫ (tan(y))4 dy
3.1.1.1
先使用 ∫ (tan(y))4 dy
5. 使用启发变换5,令z = tan(y),问题变为: ∫ z4 / (1 + z) 2 dz
6. 使用安全变换4,问题变为:∫ z2 - 1 + 1 / (1 + z2) dz
7. 使用安全变换3,问题变为:∫ z2 dz + ∫ - 1 dz + ∫ 1 / (1 + z2) dz ,此处出现了一个AND NODE,NODE上有三个叶子, (前两个叶子好解决)
8. 最后一个叶子,解决 ∫ 1 / (1 + z2) dz ,使用启发变换6,令 z = tan(t) , dz / dt = 1 + tan(z)2 ,dz = (1 + tan(z)2 ) dt, 问题变为,解决:∫ 1 dt
3.1.1.2
……