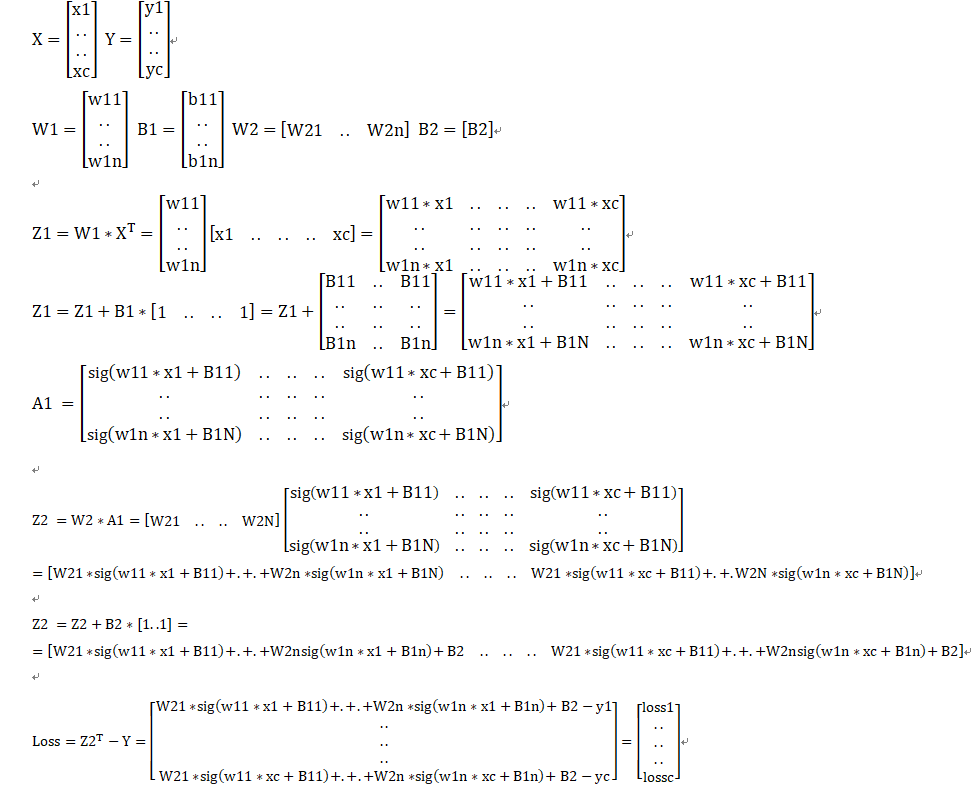
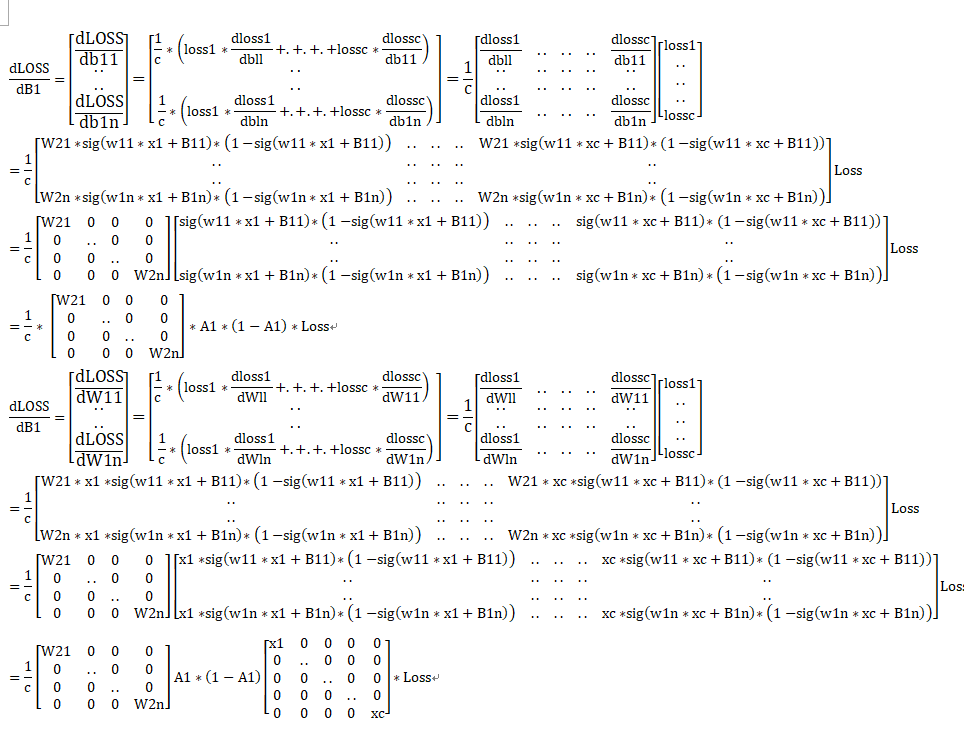
激活函数引用:https://www.cnblogs.com/ms-uap/p/9962978.html
首先,单个神经元是长这样的:
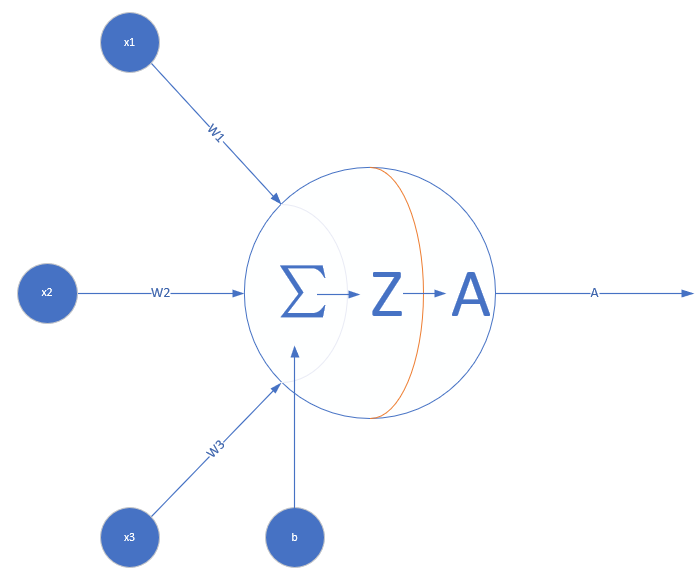
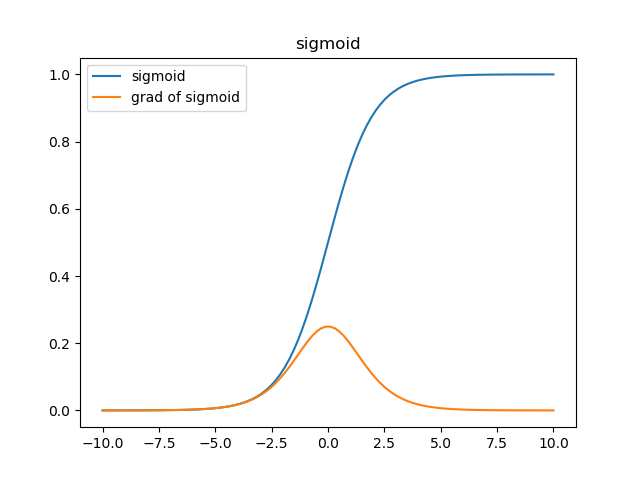
也就是,当A=σ(Z)=Z时,不使用激活函数的话,那么,单个神经网络,输出只能是A = ΣWX + b
1. 从训练数据来理解。(参考:https://blog.csdn.net/weixin_38275649/article/details/80340538)
假如我们的神经网络,仅仅是一个单细胞的神经元
联想我们的样本,例如在做图片识别的时候,通常来说,训练数据:
x1,x2,x3,是某动物的概率。(例如:有毛发:1,有獠牙:1,毛色R:255,毛色G:109,毛色B:100,是豹子的概率:0.75)
显然,如果拿A=σ(Z) = sigmoid(Z) = 0.75,看起来就很合适了(当然,强行的Z=0.75好像也没什么问题,且看第2点)
2. 从非线性组合的角度来理解。(参考:https://zhuanlan.zhihu.com/p/27661298)
在测绘中,通常我们拟合曲面的时候,有如下样本数据:
x,y,z
目标是,知道范围内的x,y,获得z。
先说一下通常的做法(我认为这是建模与神经网络训练十分重要的区别):
首先,我们假定它有一个模型:Z = w0 + w1 * x + w2 * y + w3 * x * y + w4 * x2 + w5 * y2 + w6 * x 2* y + w7 * y2 * x + w8 * x3 + w9* y3 + ……(一般就w0~w9到此为止了)
假定,(w0~w9),其初始值为(w'0~w'9),也就是:(0.1,……0.1)
假如我们使用高斯牛顿迭代法来求解,我们不直接解w0~w9,令wi = w'i +dwi,我们要解的是dwi ,也就是初始值的改正值:
原函数变为:Z = (w'0 + dw0) + (w'1+dw1) * x + (w'2 + dw2) * y + (w'3 + dw3 ) * x * y + ……;
也就是:Z = Z ' + dw0 + dw1 * x + dw2 * y + w3 * x * y + ……;
也就是:AW = (Z - Z')= b
W = [dw0,……dw9]T
而A的每一行,根据各个样本,有An = [1,x,y,xy,x2,y2 ……]
解AW=b
根据最小二乘原理,解AW=b。
ATAW=ATb
W = (ATA)-1ATb,解得W = [dw0,……dw9]T
将解的结果,代回w''i = w'i +dwi , (w''0~w''9)作为新的初始值,继续迭代解
直到:上次迭代的(Z - Z')2 和本次迭代的 (Z - Z')2 相差无几。
***如有需要以离区域中心加权,可以引入权矩阵: W = (ATPA)-1ATPb,P通常是对角阵,意思是Z与Z之间高程是独立观测量,也就是说Zi ≠ f(Zj)。
***P对角上的数值可以为 di / ∑ d,d是离中心的距离 ; 在测绘上,可以表示为 1 / (Z测量误差)2
***权值,代表我们对这个样本的关注程度,样本误差越小,权值越大。
在曲面不太复杂,且有一定的规律的时候,这种方法通常效果很理想。因为其考虑了XY之间的非线性因素。
如果以“单细胞神元” , 且激活函数A=σ(Z)=Z时,我们顶多可以 Z = WX + b , W = [w1,w2] , X = [x,y]T
这样完全只是一个空间平面而已。(w1* x + w2* y - z + b = 0)
进而,我们考虑:
A=σ(Z) = sigmoid(Z) ,参考https://zhuanlan.zhihu.com/p/27661298
根据sigmoid函数,1 / (1 + e^-z),可以看出,e^-z的泰勒展开,其实就是对x,y的非线性组合,可以解决函数仅仅为线性函数的问题。
但是:
sigmoid函数的值,只能是0~1之间,显然,我们要的Z值,肯定不是这样的(Z是根据地形,数值可能是2.xxx ,3.xxxx各种)
那么,能解决这个问题,只能是多层神经网络:https://www.cnblogs.com/ms-uap/p/10031484.html
我们的样本,其实是一个个:
(x1,y1,z1)……(xn,yn,zn)
上图仅仅是一元方程的一个样本的求法。
在引用文章当中,是逐个样本来迭代。可以将样本分为几组来迭代:
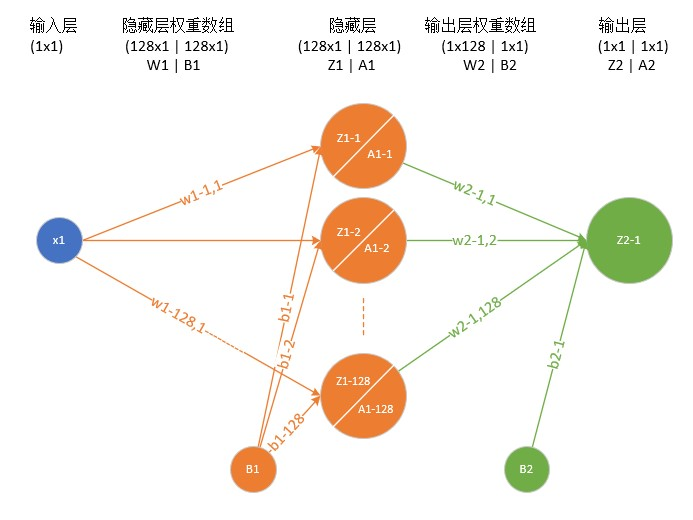
输入层,是1*2,也就是(xi,yi)
隐藏层,权重数组是128*2,那么不难理解,Z1 = WX + b
X = [ x , y ]T
Wi = [ Wi-x , Wi-y ]
bi = bi
i代表的是第几个一层神经元。
说白了,
对于一组样本:
子样本1----> 128个一层神经元------>1个二层神经元------>输出a1
子样本2----> 128个一层神经元------>1个二层神经元------>输出a2
子样本3----> 128个一层神经元------>1个二层神经元------>输出a3
子样本n----> 128个一层神经元------>1个二层神经元------>输出an
各个子样本公用同一组W1,B2,W2,B2
而损失函数,变为loss = 1 / 2 / n ∑(a - z)
那么,引用的资料中,也说明了,调参说白了,就是调整:
1. 隐藏层神经元的数量
2. 学习效率,也就是各层的步长a
3. loss阈值