平差笔记

秩：一个矩阵最大线性无关列，或者最大线性无关行；

*最大线性无关行=最大线性无关列

例如：A_mxn

求秩函数：R()；

对于A_mxn , 对于A_mxnX_nx1=0，最小二乘解A^TAX = A^Tb ，令N_nxn = A^TA，N_nxn X_nx1 = W _nx1

要使得X有唯一解，那么R(N)=n，也就是N要满秩；

因为：如果N各列线性相关，就可能有很多组X，能组合出W列向量；

R(A) = R(A^TA)，证明：

AX=0，X的所有解称为N(A)，X能构筑的空间的维度=n-R(A)；

X作为一个列向量，与A的各个行向量垂直，因此X构筑的空间⊥A的行空间

 A^TAX=0，左右乘X^T，X^TA^TAX=0（相当于同一向量求点积），此结果是向量||AX||²=0

因此：AX和A^TAX中，两个X是同解，并且对于A^TAX=0，X能构筑的空间的维度=n-R(A^TA)；

因此R(A) = R(A^TA)

由于R(A) = R(N)=n，因此：A各列必须线性无关，才可能得到AX=b最小二乘唯一解；

而对于加权最小二乘A^TPAX=A^TPB，也是一样的，因为P是对称的

---

 如果A的各列不是线性无关，也就是没有起算数据，从而导致R(N)=R(A)<min(m,n)，那么：X就不再唯一；

为了方便，将N_nxn X_nx1 = W _nx1 视为另一个形式的A_nxnX=B；

现在A_nxn不满秩，因此A^-1不存在，X的解不唯一；

---

误差传播

例一：全站仪的测方向值误差为a ，角度β = a₁ - a₂ , 那么 ：β_方差 = KD_aaK^T

 

K是β表达式中的系数矩阵，D_aa是两个观测量的协方差阵，实际上，最底层的观测值应该是线性无关的，因此非对角线上的元素的协方差为0

例二：

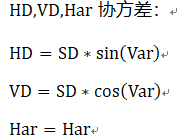
泰勒展开，使得其线性化：

 

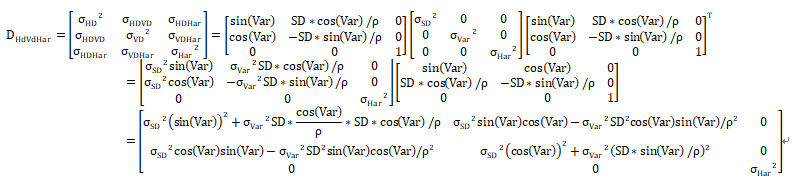
 可见，非底层的观测值，其协方差非对角线，不一定是都为0的，也就是观测值相关；

例三：

 （其实三维坐标可以以底层观测值来表示，这里只是显示误差传播的过程）

例四：

在最小二乘法当中，有加权最小二乘法，观测模型：

L = BX + d（例如：L为真边长，X为真坐标，d为方程常数项）

假设：

X = X⁰ + x

L = L⁰ + V 

L⁰ 为观测值，X⁰为坐标近似值，x为坐标改正数，l为观测值改正数

为了使得：

误差：

V = L - L⁰

   = B(X⁰ + x) + d - L⁰

   = Bx -  (BX⁰ + d  - L⁰)

   = Bx - l

BX⁰ + d  就是观测值的近似值，因此 l 就是近似值与观测值之差

那么，平差的目标，是为了使得向量V的长度最小，也就是 |V|²= v₁v₁ + v₂v₂ + .....最小

但是，并不是每个V_n 的可信性都是一样的，因为每个L⁰的可信度不一样，就要加权，变成要求|V|²= p₁v₁v₁ + p₂v₂v₂ + .....最小，也就是V^TPV最小

可信度越高，p越大，可见，使用L_i的方差倒数，方差越小，权越大，是一个不错的选择；

（注意，当L0相互不独立时，还要加上p₁₂V₁V₂ + p₁₃V₁V₃ + ....）

按照上面的推论，也就是：

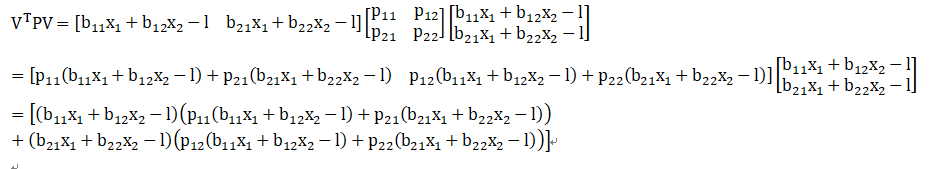
 也就是解方程组：

d(V^TpV)/dx₁ = 0

d(V^TpV)/dx₂ = 0

上面方程组可以写为：

B^TPV = B^TPBx - B^TPl = 0 

也就是解 B^TPBx = B^TPl

---

用纯粹线性代数的概念，假如