PCA算法及其应用
1.主成分分析(PCA)
1.主成分分析(Principal Component Analysis,PCA) 是最常用的一种降维方法,通常用于高维数据集的探索与可视化,还可以用做数据压缩和预处理等。
2.PCA可以把具有相关性的高维变量合成为线性无关的低维变量,称为主成分。主成分能够尽可能保留原始数据的信息。
在介绍PCA的原理之前需要回顾涉及到的相关术语:
1.方差:
2.协方差
3.协方差矩阵
4.特征向量和特征值
方差:是各个样本和样本均值的差的平方和的均值,用来度量一组数据的分散程度。公式为:
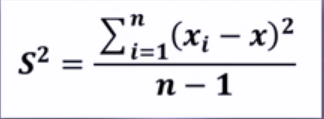
协方差: 用于度量两个变量之间的线性相关性程度,若两个变量的协方差为0,则可认为二者线性无关。协方差矩阵则是由变量的协方差值构成的矩阵(对称阵)。公式为:
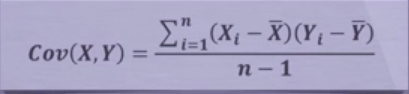
特征向量:矩阵的特征向量是描述数据集结构的非零向量,并满足如下公式:

2.原理
原理:矩阵的主成分就是其协方差矩阵对应的特征向量,按照对应的特征值大小进行排序,最大的特征值就是第一主成分,其次是第二主成分,以此类推。其详细推导过程可以参见周志华老师编写的<<机器学习>>那本书。
主成分分析----算法过程

那么我们如何使用sklearn中提供的PCA函数呢?如下所示:
3.sklearn中主成分分析
在sklearn库中,可以使用sklearn.decomposition.PCA加载PCA进行降维,主要参数有:
1.n_components:指定主成分的个数,即降维后数据的维度。
2.svd_solver:设置特征值分解的方法,默认为:'auto',其他可选有'full','arpack','randomized'
4.PCA实现高维数据可视化

实例程序编写:



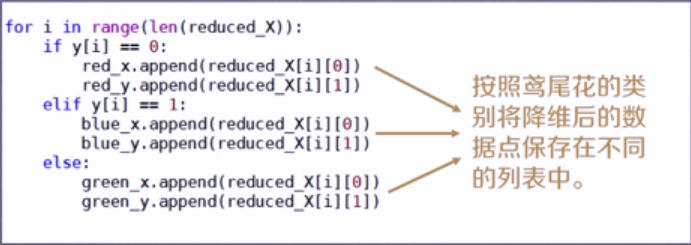

即调用scatter函数进行数据的可视化!
5.结果展示: