这篇文章用来整理一下入门深度学习过程中接触到的四种激活函数，下面会从公式、代码以及图像三个方面介绍这几种激活函数，首先来明确一下是哪四种：
-
Sigmoid函数
-
Tahn函数
-
ReLu函数
-
SoftMax函数
激活函数的作用
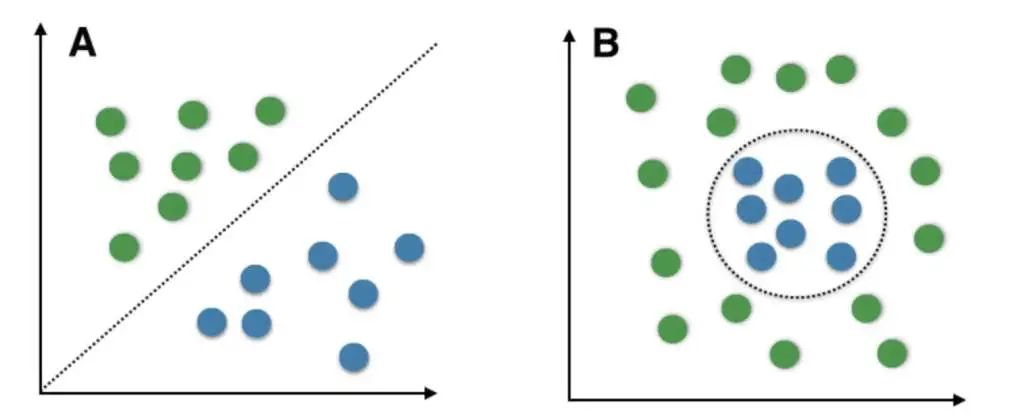
下面图像A是一个线性可分问题，也就是说对于两类点(蓝点和绿点)，你通过一条直线就可以实现完全分类。
当然图像A是最理想、也是最简单的一种二分类问题，但是现实中往往存在一些非常复杂的线性不可分问题，比如图像B，你是找不到任何一条直线可以将图像B中蓝点和绿点完全分开的，你必须圈出一个封闭曲线。
而激活函数就是帮助"绘制"这个封闭曲线的非线性函数，有了激活函数的帮助，很多算法的处理能力会得到加强，也可以处理线性不可分问题。
Sigmoid函数
Sigmoid函数曾在介绍逻辑回归时提起过，它的数学表达式为：
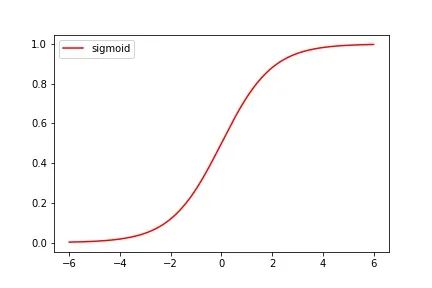
其中 e 为纳皮尔常数，其值为2.7182... 它的图像如下：
可以观察出图像的一些特点：
-
曲线的值域为(0,1)
-
当x = 0时，Sigmoid函数值为0.5
-
随着 x 不断增大，Sigmoid函数值无限趋近于1
-
随着 x 不断减小，Sigmoid函数值无限趋近于0
对于梯度下降法而言，信息的更新很大程度上都取决于梯度，而Sigmoid函数一个很明显的缺点就是当函数值特别靠近0或1这两端时，因为它的曲线已经近乎平缓，所以此时的梯度几乎为0，这样非常不利于权重的更新，从而就会导致模型不收敛。
Sigmoid函数的代码如下：
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))Tanh函数
Tanh函数是双曲正切函数，它的的数学表达式为：
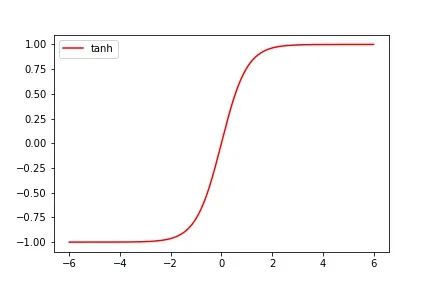
Tanh函数和Sigmoid函数非常相近，这点从图像上可以很好的体现：
这两个函数相同的是，当输入的 x 值很大或者很小时，对应函数输出的 y 值近乎相等，同样的缺点也是梯度特别小，非常不利于权重的更新；不同的是Tanh函数的值域为(-1,1)，并且当 x = 0 时，输出的函数值为0。
Tanh函数的代码如下：
import numpy as np
def tanh(x):
return (exp(x)-exp(-x))/(exp(x)+exp(-x))ReLu函数
ReLu是线性整流函数，又称为修正性线性单元，它的函数的数学表达式为
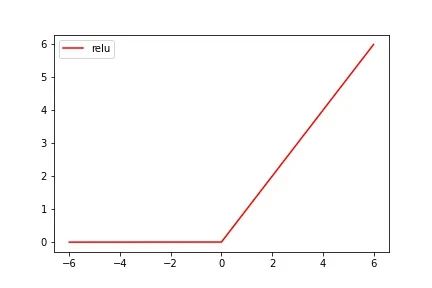
Tanh是一个分段函数，它的图像如下：
图像很容易理解，若输入的 x 值小于0，则输出为也为0；若输入的 x 值大于0，则直接输出 x 值，需要注意的是ReLu函数在x = 0 处不连续(不可导)，但同样也可以作为激活函数。
与Sigmoid函数和Tanh函数相比，ReLu函数一个很明显的优点就是在应用梯度下降法是收敛较快，当输入值为整数时，不会出现梯度饱和的问题，因为大于0的部分是一个线性关系，这个优点让ReLu成为目前应用较广的激活函数。
ReLu函数的代码如下：
import numpy as np
def relu(x):
return np.maximum(0,x)SoftMax函数
分类问题可以分为二分类问题和多分类问题，Sigmoid函数比较适合二分类问题，而SoftMax函数更加适合多分类问题。
SoftMax函数的数学表达式为：
其中表示分类器的输出，i表示类别索引，总的类别个数为C，表示当前元素的指数与所有元素指数和的比值。概括来说，SoftMax函数将多分类的输出值按比例转化为相对概率，使输出更容易理解和比较。
为了防止SoftMax函数计算时出现上溢出或者下溢出的问题，通常会提前对 V 做一些数值处理，即每个 V 减去 V 中的最大值，假设，SoftMax函数数学表达式更改为：
因为SoftMax函数计算的是概率，所以无法用图像进行展示，SoftMax函数的代码如下：
import numpy as np
def softmax(x):
D = np.max(x)
exp_x = np.exp(x-D)
return exp_x / np.sum(exp_x)