在数据探索工作中,作为数据特征分析的角度,对比分析、统计量分析同样是发掘数据间关系与数据特征的重要渠道。
1 对比分析
对比分析是指把两个相互联系的指标进行比较,从数量上展示和说明研究对象规模的大小,水平的高低,速度的快慢等,主要强调各角度的“比较”。
对比分析主要有以下两种形式:
1)绝对数比较
适合指标在量级上不能差别过大,常用折线图、柱状图。
2)相对数比较
包括结构分析、比例分析、空间比较分析、动态对比分析等,例如:
结构相对数:将同一总体内的部分数值与全部数值对比求得比重,用以说明事物的性质、结构或质量。如居民食品支出额占消费支出总额比重、产品合格率等。
比例相对数:将同一总体内不同部分的数值进行对比,表明总体内各部分的比例关系。如人口性别比例、投资与消费比例等。
比较相对数:将同一时期两个性质相同的指标数值进行对比,说明同类现象在不同条件下的数量对比关系。如不同行业、不同企业间某项指标对比等。
动态相对数:将同一现象在不同时期的指标数值进行对比,用以说明发展发向和变化的速度。如发展速度、增长速度。
由于数据的对比所涉范围极其宽广,各种可能的对比角度均可执行,所以从哪个方面进行对比还得依赖实际问题与关注点,本文不再示例。
2 统计量分析
统计量分析用于检查数据特征,把握数据整体的性质,包括检查数据的集中程度、离散程度和分布形状,通过这些统计量可以从整体上把握数据的重要性质。
2.1 集中趋势
常用指标有均值、中位数、众数等。
2.2 离中趋势
常用指标有标准差、四分位间距、极差、变异系数等。
python中已内置了描述上述统计量的方法:
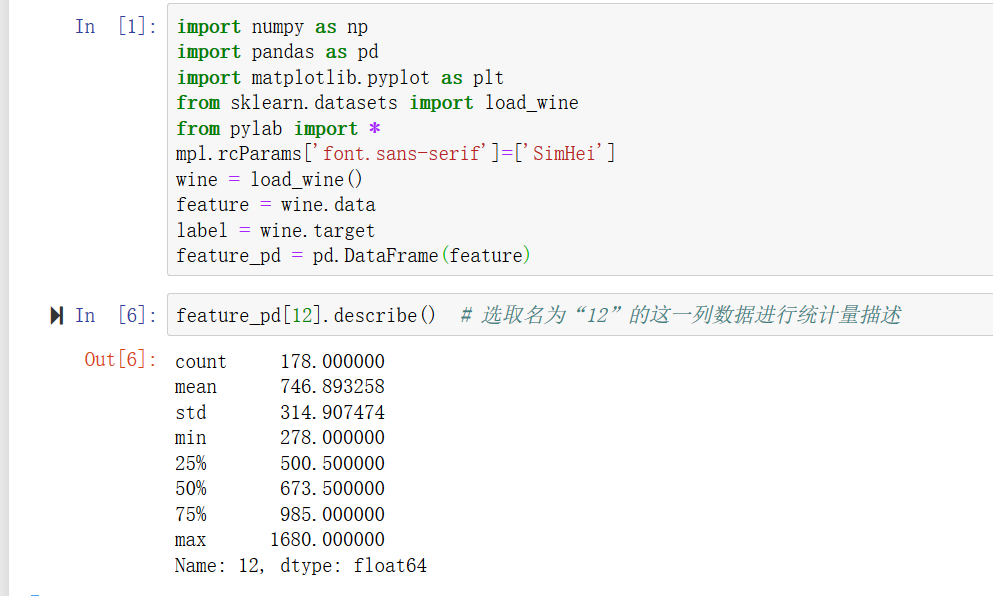
2.3 分布形状
分布形状使用偏度系数和峰度系数来度量,
偏度系数是用于衡量数据分布对称性的统计量,反映数据分布偏移中心位置的程度。正态分布的偏度为0;偏度<0称分布具有负偏离(左偏态),此时数据位于均值左边的比右边的多,有个尾巴拖到左边,说明左边有极端值;偏度>0称分布具有正偏离(右偏态);偏度接近于0 ,认为分布对称。例如:分布有可能在偏度上偏离正态分布,则可用偏度来检验分布的正态性。偏度的绝对值数值越大表示其分布形态的偏斜程度越大。
峰度系数是用于衡量数据分布陡峭或平滑的统计量,判定数据分布相对于正态分布而言是更陡峭还是平缓。例如:正态分布的峰度系数值是3;K>3的峰度系数说明观察量更集中,有比正态分布更短的尾部;K<3的峰度系数说明观测量不那么集中,有比正态分布更长的尾部。
关于偏度与峰度的进一步阐释可以参考这篇博客:https://blog.csdn.net/u012735708/article/details/84750295