ST表学习笔记

看神仙学长的博客学的：传送门

st表介绍：

功能:

它是解决区间最值问题的一种强有力的数据结构（雾我也不知道应不应该叫数据结构）

它可以做到O(nlogn)预处理，O(1)查询最值

原理：

把给定区间分成长度是2的幂次的小区间。先预处理出它们中的最小值是多少,然后用一种类似二分的思想由小区间到大区间比较两个区间的最小值。

倍增算法：

倍增讲解

不会的数学公式就只能截图了，咕咕咕....

**好像还是不太懂边界，我果然太菜了，咕咕咕.....，只能背了

实现：

变量：

1.f[i][j] : 记录给定序列中区间[i,i+pow(2,j)-1]中的最大值。 ps:f[i][0]=a[i]
2.bit[i] : bit[i]=pow(2,i)-----记录2的i次方 可以用位运算<<代替，不过一定要加()，否则就咕咕咕了
3.a[i] :输入的数组
4.LC:在生成st表时作为f[i][j]中j的循环上界。

例子：

设有一长度为5的a数组：a1,a2,a3,a4,a5
长度为1的区间[1,1],[2,2],[3,3],[4,4],[5,5]

长度为2的区间[1,2],[2,3],[3,4],[4,5]

长度为4的区间[1,4],[2,5]

用f[i][j]表示：f[i][j]=[i,i+pow(2,j)-1]

长度为1的区间: f[1][0] <=>[1,1]

f[2][0] <=>[2,2]

长度为2的区间： f[1][1] <=>[1,2]

f[2][1] <=>[2,3]

f[1][2] <=>[1,4]

f[2][2] <=>[2,5]

如何求得f[i][j]的值：

f[i][j]=max(f[i][j-1],f[i+pow(2,j-1)][j-1]);

模板：

题目：

P3865 【模板】ST表

题目描述:给定一个长度为 N 的数列，和 M 次询问，求出每一次询问的区间内数字的最大值。

代码：

第一次提交:

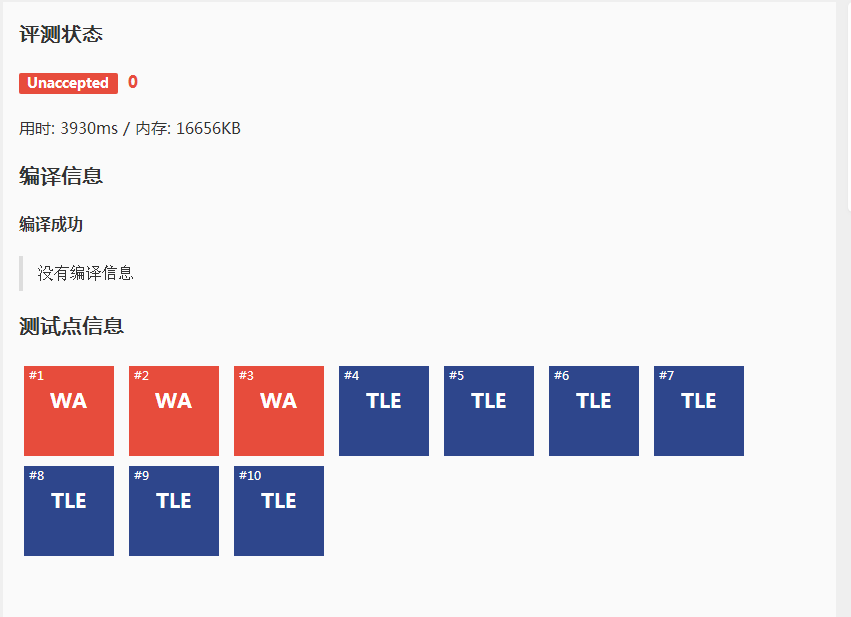
检查了检查发现i和j写反了，咕咕咕

NM还是TLE，lzt和我查了好长时间错误后，发现数组开大了，咕咕咕咕.....
真是活久见了数组大了竟然能tle而不是mle

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<string>
#include<cstring>
#define ll long long int
#define MAXN 100001
using namespace std;
const int maxn=999999999;
const int minn=-999999999;
inline int read() {
	char c = getchar(); int x = 0, f = 1;
	while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
	while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
	return x * f;
}
int f[MAXN][41],a,lc,n,m,p,len,l,r;
int main()
{
	n=read(),m=read();
	for(int i=1;i<=n;++i) a=read(),f[i][0]=a;
	lc=(int)(log(n)/log(2));
	for(int j=1;j<=lc;++j)
	{
		for(int i=1;i<=n-(1<<j)+1;i++)
		{
			f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
		}
	}
	for(int i=1;i<=m;++i)
	{
		l=read(),r=read();
		p=(int)(log(r-l+1)/log(2));
		cout<<max(f[l][p],f[r-(1<<p)+1][p])<<'
';
	}
	return 0;
}