NOI1999]生日蛋糕

目录

• 题目链接
• 思路
• 总结：
• 代码

题目链接

P1731 [NOI1999]生日蛋糕

思路

搜索+剪枝

用(mins[i])表示第(i)层最小的表面积(minv[i])表示第(i)层最小体积，设最底层为第(n)层，枚举每一层的高和半径。

不过复杂度这样复杂度上天

所以要加上优化（剪枝）

我们先来看一下下题目中的几个细节：

当(i<M)时，要求(R_i>R_{i+1}且H_i>H_{i+1})

这句好就告诉我们一个事情，当我们枚举半径和高度时是可以确定上下界的，这就是剪枝一

第二个细节

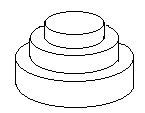
看一下这个图就会发现最下面那一层的底面积是不是就是上面的上表面积之和(也就是下图涂黑的地方)

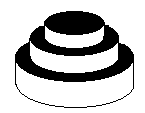
这么看来我们只要枚举到最下层是记录一下(i imes i)就不用考虑涂黑的部分了，简化了程序

再看其他的剪枝:

1.如果当前搜索到的最小表面积已经大于了已知的最小表面积直接退出
2.如果当前搜索到的体积已经超过题目限制，则退出
3.如果由体积推出来当前的表面积已经不优直接退出

总结：

1.枚举半径和高度时是可以确定上下界
2.如果当前搜索到的最小表面积已经大于了已知的最小表面积直接退出
3.如果当前搜索到的体积已经超过题目限制则退出
4.如果由体积推出来当前的表面积已经不优直接退出

代码

#include<bits/stdc++.h>
using namespace std;
//体积公式:v=piRH
//侧面积:2piRH
//底面积:piR^2
const int MAXN=0x3f3f3f;
const int N=20007;
int ans=MAXN;
int mins[N],minv[N],n,m;
void dfs(int now,int r,int h,int s,int v) {
	//  当前层数 半径  高度 面积  体积
	int MAXN_high=h;
	if(now==0) {
		if(v==n) {
			ans=min(ans,s);
		}
		return ;
	}
	if(s+mins[now-1]>=ans) return ;//如果面积已经大于了目前的最优值ans就可以退出了
	if(v+minv[now-1]>n) return;//如果当前搜到的体积已经大于了题目给定的体积就可以退出了
	if(2*(n-v)/r+s>=ans)  return; //由体积推出的表面积已经大于最大值了就可以退出了
	for(int i=r-1; i>=now; --i) {//枚举半径
		if(now==m) s=i*i;//此处是处理最下面的那个面其实也就是上面的那个，可以看一下解释
		MAXN_high=min(h-1 ,(n-minv[now-1]-v)/i/i);//求出最大的高度来
		for(int j=MAXN_high; j>=now; --j) {
			dfs(now-1,i,j,s+2*i*j,v+i*i*j);
		}
	}
}
int main() {
	cin>>n>>m;
	/*初始化每层成最小的表面积和体积*/
	for(int i=1; i<=m; ++i) {
		mins[i]=mins[i-1]+2*i*i;//计算面积
		minv[i]=minv[i]+i*i*i;//计算体积
	}
	dfs(m,n,n,0,0);//开始dfs喽
	if(ans==MAXN) cout<<0<<'
';
	else cout<<ans<<'
';
	return 0;
}