Luogu P2096 最佳旅游线路

题目描述

某旅游区的街道成网格状。其中东西向的街道都是旅游街，南北向的街道都是林阴道。由于游客众多，旅游街被规定为单行道，游客在旅游街上只能从西向东走，在林阴道上则既可从南向北走，也可以从北向南走。

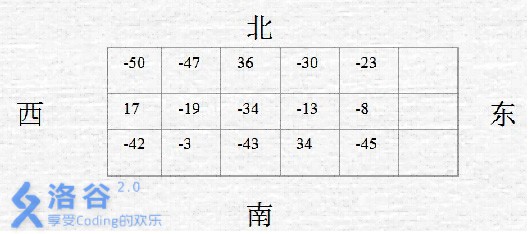
阿龙想到这个旅游街游玩，他的好友阿福给了他一些建议，用分值表示所有旅游街相邻两个路口之见的街道值得游览的程度，分值是从-100到100的整数，所有林阴道不打分。所有分值不可能全是负分。如图：

输入输出格式

输入格式：

输入文件的第一行是两个整数m和n,之间用一个空格隔开，m表示有m条旅游街（1≤m≤100 ），n 表示有(n+1)条林阴道（1≤n≤20001 ）。接下来的m行依次给出了由北向南每条旅游街的分值信息。每行有n个整数，依次表示了自西向东旅游街每一小段的分值。同一行相邻两个数之间用一个空格隔开。

输出格式：

输出文件只有一行，是一个整数，表示你的程序找到的最佳游览线路的总分值。

输入输出样例

输入样例#1：

3 5 
-50  –47  36   –30  –23 
17   –19  –34  –13  –8 
-42  –3   –43  34   -45 

输出样例#1：

84

Solution

大致就是找出每列最大值，再求最大子段和……

（但我拿出一个自认为时间复杂度（虽然读入的时间复杂度最大QAQ）、空间复杂度较小的方法……（应该是吧QAQ））

——————分割不完全的分割线——————

pascal程序如下：

var n,m,i,j,k,max:longint;
a:array[0..20001]of longint;//一个20000的数组就够了
begin
  readln(n,m);
  for i:=1 to m do
  a[i]:=-maxlongint;//定初始值，方便下面选最大值
  for i:=1 to n do
  for j:=1 to m do//读入的时间复杂度最大QAQ
  begin
    read(k);
    if k>a[j] then//选最大值
    a[j]:=k;
    //千万不能readln，第八个点坑爹，切记！
  end;
  k:=0;
  max:=-maxlongint;
  for i:=1 to m do//求最大子段和
  begin
    if a[i]+k<0 then//如果加到一个数和比0小，还能要吗！！！
    k:=0//不能要
    else
    k:=k+a[i];//能要
    if k>max then//找最大值
    max:=k;
  end;
  writeln(max);
end.