树状数组初步理解

 

学习树状数组已经两周了，之前偷懒一直没有写，赶紧补上防止自己忘记（虽然好像已经忘得差不多了）。
作为一种经常处理区间问题的数据结构，它和线段树、分块一样，核心就是将区间分成许多个小区间然后通过对大区间的调用来提升效率。因此，我们主要需要了解的就是这种分块方式。
不同于线段树直接将区间不断的进行二分，我们将区间二分的同时将父节点直接放在右区间上，从而形成了一个占用空间很小的树。

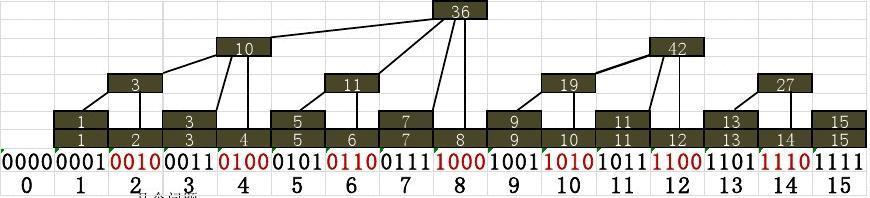
我们仔细观察这张图：根据我们刚才的思想，每个右节点都储存着左右两个子区间的和，即右节点本身就是自己的父节点，而右节点的父节点就是父节点的父节点。想象一下，原本是一个立体的二叉树，我们现在将它向右压，硬生生将一个二维的树压成了一个数组，就得到——树状数组！！！
虽然占用空间大大减小，但是对结点的访问现在变成了一个问题，我们应该怎么访问父亲结点和子节点呢？
仔细观察，我们发现结点n是x个结点的祖先，这个x就是n的二进制的不为零的最小位（不要问我为什么能看出来，我也看不出来啊，也不知道哪位神仙想出来的），我们用一个函数lowbit(n)来表示这个神奇的数字。因为父节点是右偏的（杜撰的专业术语233），所以右边lowbit(n)个元素和这个区间是并列的，并且右边lowbit(n)长的区间最右边的元素是左右两个区间的祖先，它的位置我们很容易得到是n+lowbit(n)——这就是子节点到父节点的访问方式。
结点n是左边lowbit(n)个元素的祖先，所以n-lowbit(n)就是另外一个与n所在区间紧邻而且没有重叠的区间，所以我们想要遍历n以前所有的元素时只需要不断的进行n-lowbit(n)直到n==0表示已经跳出区间，通过这种方法我们能够方便的得到前缀和。
通过上面的总结，我们得到了对树状数组进行访问的初步方法。
lowbit()函数的实现方式一般开来说时lowbit(x)=x&(-x);至于为什么这就涉及到玄学的二进制知识，有兴趣的话自己去了解一下吧。
根据以上分析，我们可以得到初步的对树状数组建立以及维护的方法：
假如我们想要得到的是区间求和：

int lowbit(x)
{
	return x&(-x);
}
void update(int x,int y)
{
	for(;x<=n;x+=lowbit(x))	//x+lowbit(x)是包含x元素的父节点 
	{
		c[x]+=y;
	}
}

如何进行查询呢？

int sum(int x)	//x的前缀和 
{
	int ans=0;
	for(;x;x-=lowbit(x))
	{
		ans+=c[x];
	}
	return ans;
} 

如果想要得到中间一段区间的和，不难想到query(x,y)=sum(y)-sum(x-1);
这样，我们就初步实现了树状数组的维护和查询。
下附一道练手题：
POJ - 2352 Stars
大概意思就是说求一个二维数组中处于左下角的元素的个数。乍一看好像是一个二维的树状数组，但是分析一下数据范围就会发现不太现实。而且题目中说给出的数据是有顺序的，因此我们可以分析一下，不难发现（就当作不难吧）后面输入的数据对前面输入的数据是没有影响的，而且对于每一颗星星来讲，处于它下方右边的并没有什么意义，因此我们不妨将这个图形一维化，每个星星的亮度就是所有处于它左边（和它所在位置但不包括它）星星的个数。问题的思路应该很清晰，下附ac代码：

#include<cstdio>
#include<cstring>
using namespace std;

const int maxn=32005;
int n;
int c[maxn];
int ans[maxn];

int lowbit(int x)
{
	return x&(-x);
}
void update(int x)
{
	for(;x<=maxn;x+=lowbit(x))
	{
		c[x]++;
	}
}
int sum(int x)
{
	int ans=0;
	for(;x;x-=lowbit(x))
	{
		ans+=c[x];
	}
	return ans;
}
int main()
{
	int u,v;
	memset(c,0,sizeof(c));
	memset(ans,0,sizeof(ans));
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&u,&v);
		u++;//需要注意树状数组的下标必须从1开始！！！
		ans[sum(u)]++;
		update(u);
	}
	for(int i=0;i<n;i++)
	{
		printf("%d
",ans[i]);
	}
	return 0;
}

至于树状数组的区间修改区间查询，将会在树状数组的进一步理解中说明。