我们都知道java中有封装好的方法,用来比较A字符串是否包含B字符串
如下代码,contains,用法是 str1.contains(str2), 这个布尔型返回,存在返回true,不存在返回false
还有indexOf,用法和contains一致,返回值是int,存在则返回对应的位置,注意位置从0开始的,不存在返回-1
public class Test {
public static void main(String[] args) {
String source = "abacaabacabacabaabb";
String pattern = "abacab";
System.out.println(source.contains(pattern) ); //true
System.out.println(source.indexOf(pattern) ); //5
}
}
这两个方法的具体实现,是在java.lang包中,最终类String下
public boolean contains(CharSequence s) {
return indexOf(s.toString()) > -1;
}
contains其实调用了indexOf
public int indexOf(String str) { return indexOf(str, 0); }
public int indexOf(String str, int fromIndex) { return indexOf(value, 0, value.length, str.value, 0, str.value.length, fromIndex); }
static int indexOf(char[] source, int sourceOffset, int sourceCount, char[] target, int targetOffset, int targetCount, int fromIndex) { if (fromIndex >= sourceCount) { return (targetCount == 0 ? sourceCount : -1); } if (fromIndex < 0) { fromIndex = 0; } if (targetCount == 0) { return fromIndex; } char first = target[targetOffset]; int max = sourceOffset + (sourceCount - targetCount); for (int i = sourceOffset + fromIndex; i <= max; i++) { /* Look for first character. */ if (source[i] != first) { while (++i <= max && source[i] != first); } /* Found first character, now look at the rest of v2 */ if (i <= max) { int j = i + 1; int end = j + targetCount - 1; for (int k = targetOffset + 1; j < end && source[j] == target[k]; j++, k++); if (j == end) { /* Found whole string. */ return i - sourceOffset; } } } return -1; }
如果你没有去看java中自带的实现,要你自己写方法实现呢
这就涉及到了算法:算法就是你的思路=======
第一步: 先构思一下思路,我要怎么去比较;一般人的思路是:
我拿后者的第一个字符,去看前者中是否含有,如果米有,一定不匹配;
我拿后者的第一个字符,去看前者中是否含有,如果前者中含有,继续查看,第二个字符是否和长串中接下来的一个字符相等
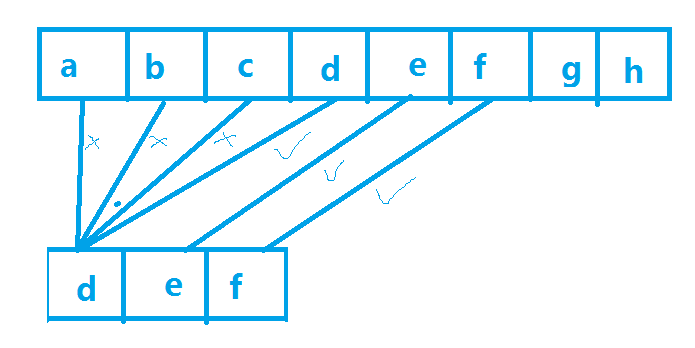
相等,继续向下匹配(如下图一)
不相等,重新用后者的第一个字符再和长字符串接下来一位进行比较
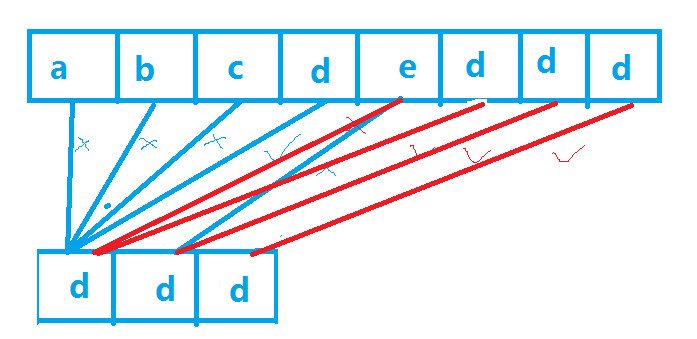
何谓接下来一位呢【假设abcdefgh和ddd,第一次比配到长字符串的第四位相等,第二次和长字符串的第5位开始比较,如下图二】
public class Force { /** * 暴力匹配 * 时间复杂度为O(n*m);n为主串长度,m为模式串长度 算法的基本思想: 从主串的起始位置(或指定位置)开始与模式串的第一个字符比较,若相等,则继续逐个比较后续字符; 否则从主串的下一个字符再重新和模式串的字符比较。 依次类推,直到模式串成功匹配,返回主串中第一次出现模式串字符的位置,或者模式串匹配不成功,返回不成功,实际中可将返回值设置为int,不成功返回-1,成功返回0; * @param source * @param pattern * @return */ public static String bruteForceStringMatch(String source, String pattern) { int slen = source.length(); int plen = pattern.length(); char[] s = source.toCharArray(); char[] p = pattern.toCharArray(); int i = 0; int j = 0; if (slen < plen) return "你瞧瞧主串长度小于模式串,怎么可能啊,匹配失败"; // 如果主串长度小于模式串,直接返回-1,匹配失败 else { while (i < slen && j < plen) { if (s[i] == p[j]) // 如果i,j位置上的字符匹配成功就继续向后匹配 { System.out.println(i+ "的值是"+ s[i] ); System.out.println(j + "的值是"+ p[j]); ++i; ++j; } else { System.out.println("我是else下的" + i + "的值是"+ s[i] ); System.out.println("我是else下的" + j + "的值是"+ p[j]); i = i - (j - 1); // i回溯到主串上一次开始匹配下一个位置的地方 j = 0; // j重置,模式串从开始再次进行匹配 } } if (j == plen) // 匹配成功 return "位置是"+(i+1 - j); else return "匹配失败"; // 匹配失败 } } }
查看匹配结果:


这是暴力破解,abcdeddd和ddd,在ddd的第0位和abcdeddd的第3位匹配后,继续比较下一位,发现不匹配了,重新将ddd的第0位和
kmp的思路如下:
KMP算法
KMP算法是D.E.Knuth、V.R.Pratt和J.H.Morris同时发现,所以命名为KMP算法。
此算法可以在O(n+m)的时间数量级上完成串的模式匹配。
主要就是改进了暴力匹配中i回溯的操作,KMP算法中当一趟匹配过程中出现字符比较不等时,
不直接回溯i,而是利用已经得到的“部分匹配”的结果将模式串向右移动(j-next[k])的距离。
import java.util.Arrays; public class kmp { /** * KMP算法 KMP算法是D.E.Knuth、V.R.Pratt和J.H.Morris同时发现,所以命名为KMP算法。 此算法可以在O(n+m)的时间数量级上完成串的模式匹配。 主要就是改进了暴力匹配中i回溯的操作,KMP算法中当一趟匹配过程中出现字符比较不等时, 不直接回溯i,而是利用已经得到的“部分匹配”的结果将模式串向右移动(j-next[k])的距离。 * @param source * @param pattern * @return */ public static String kmpStringMatch(String source, String pattern) { int i = 0; int j = 0; char[] s = source.toCharArray(); char[] p = pattern.toCharArray(); int slen = s.length; int plen = p.length; int[] next = getNext(p); while(i < slen && j < plen) { if(j == -1 || s[i] == p[j]) { ++i; ++j; } else { //如果j != -1且当前字符匹配失败,则令i不变, //j = next[j],即让pattern模式串右移j - next[j]个单位 j = next[j]; } } if(j == plen) return "位置是"+(i+1 - j); else return "匹配失败"; // 匹配失败 } /** * 关于next[k]数组的计算引出的两种办法,一种是递归,一种对递归优化,第一种对应的就是KMP算法,第二种就是优化的KMP算法。 next函数值仅取决于模式串本身而和主串无关。 有很多讲next函数值计算办法的资料,在此我想用一种直观的比较容易理解的办法来表达。 举个栗子:现在有一个模式串abab 模式串的各个字串 前缀 后缀 最大公共元素长度 a null null 0 ab a b 0 aba a,ab a,ba 1 abab a,ab,aba b,ab,bab 2 * @param p * @return */ private static int[] getNext(char[] p) { /** * 已知next[j] = k, 利用递归的思想求出next[j+1]的值 * 1.如果p[j] = p[k],则next[j+1] = next[k] + 1; * 2.如果p[j] != p[k],则令k = next[k],如果此时p[j] == p[k],则next[j+1] = k+1 * 如果不相等,则继续递归前缀索引,令k=next[k],继续判断,直至k=-1(即k=next[0])或者p[j]=p[k]为止 */ int plen = p.length; int[] next = new int[plen]; System.out.println("next函数值:" + Arrays.toString(next)); int k = -1; int j = 0; next[0] = -1; //这里采用-1做标识 while(j < plen -1) { if(k == -1 || p[j] == p[k]) { ++k; ++j; next[j] = k; } else { k = next[k]; } } System.out.println("next函数值:" + Arrays.toString(next)); return next; } }