列表、元祖、集合、字典解析式

列表解析式

[expr for iter_item in iterable if cond_expr]

List_e = [ x ** 2 for x in range(10) ]
List_e 
#结果：[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
List_f = []
for x in range(10):
    List_f.append( x ** 2 )    
List_f
#结果：[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
List_g = list(map(lambda x:x ** 2,range(10)))
List_g
#结果：[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

嵌套列表解析式

使用列表推导式嵌套时，需要注意前后调用关系。前推导式的值需要在后面书写才能生效。

需要输出的值放到推导式的最前面，生成输出值的推导式在最后面

list_1 = [[1, 2, 3], [4, 5, 6]]
list_2 = [i*2 for list_inside in list_1 for i in list_inside*2]
list_3 = []
for list_inside in list_1:
    for i in list_inside*2:
        list_3.append(i*2)
print(list_2)
print(list_3)

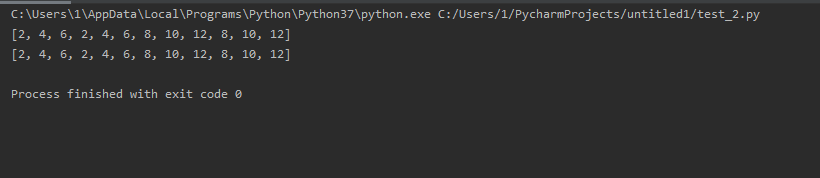
 说明：

不建议使用多重嵌套，阅读带来障碍。可以考虑使用for循环。

进行行列互换

matrix = [ [1, 2, 3, 4],
           [5, 6, 7, 8],
           [9, 10, 11, 12],
        ]
len_1 = len(matrix[0])
list_2 = [[row[i] for row in matrix] for i in range(len_1)]
print(list_2)

　

• 列表解析支持多重嵌套
• 列表解析支持多重迭代
• 列表解析语法中的表达式可以是简单表达式，也可以是复杂表达式，甚至是函数列表解析语法中的表达式可以是简单表达式，也可以是复杂表达式，甚至是函数
• 列表解析语法中的 iterable 可以是任意可迭代对

推荐在需要生成列表的时候使用列表解析

• 使用列表解析更为直观清晰，代码更为简洁

• 列表解析的效率更高（对于大数据处理，列表解析并不是一个最佳选择，过多的内存消耗可能会导致 MemoryError ）

元组解析式

（ expr for iter_item in iterable if cond_expr  ）

也可以将元祖转化为列表在进行处理，处理完成后再转化成元祖

集合解析式

 {expr for iter_item in iterable if cond_expr }

也可以将集合转化为列表在进行处理，处理完成后再转化成集合

字典解析式

{key_ expr:valuse_expr for iter_item in iterable if cond_expr }

dict_1 = dict([('a', 1), ('b', 2), ('c', 3)])
dict_2 ={key+'S': values**2 for key, values in dict_1.items() if values >= 2}
print(dict_2)