Python机器学习(7)——SVM支持向量机

SVM支持向量机是建立于统计学习理论上的一种分类算法，适合与处理具备高维特征的数据集。

SVM算法的数学原理相对比较复杂，好在由于SVM算法的研究与应用如此火爆，CSDN博客里也有大量的好文章对此进行分析，下面给出几个本人认为讲解的相当不错的：

支持向量机通俗导论（理解SVM的3层境界）：http://blog.csdn.net/v_july_v/article/details/7624837

JULY大牛讲的是如此详细，由浅入深层层推进，以至于关于SVM的原理，我一个字都不想写了。。强烈推荐。

还有一个比较通俗的简单版本的：手把手教你实现SVM算法：http://blog.csdn.net/alvine008/article/details/9097105

SVN原理比较复杂，但是思想很简单，一句话概括，就是通过某种核函数，将数据在高维空间里寻找一个最优超平面，能够将两类数据分开。

针对不同数据集，不同的核函数的分类效果可能完全不一样。可选的核函数有这么几种：

线性函数：形如K(x,y)=x*y这样的线性函数；

多项式函数：形如K(x,y)=[(x·y)+1]^d这样的多项式函数；

径向基函数：形如K(x,y)=exp(-|x-y|^2/d^2）这样的指数函数；

Sigmoid函数：就是上一篇文章中讲到的Sigmoid函数。

我们就利用之前的几个数据集，直接给出Python代码，看看运行效果：

测试1：身高体重数据

# -*- coding: utf-8 -*-
import numpy as np
import scipy as sp
from sklearn import svm
from sklearn.cross_validation import train_test_split
import matplotlib.pyplot as plt
 
data   = []
labels = []
with open("data\1.txt") as ifile:
        for line in ifile:
            tokens = line.strip().split(' ')
            data.append([float(tk) for tk in tokens[:-1]])
            labels.append(tokens[-1])
x = np.array(data)
labels = np.array(labels)
y = np.zeros(labels.shape)
y[labels=='fat']=1
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.0)
 
h = .02  
# create a mesh to plot in
x_min, x_max = x_train[:, 0].min() - 0.1, x_train[:, 0].max() + 0.1
y_min, y_max = x_train[:, 1].min() - 1, x_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
 
''' SVM '''
# title for the plots
titles = ['LinearSVC (linear kernel)',
          'SVC with polynomial (degree 3) kernel',
          'SVC with RBF kernel',
          'SVC with Sigmoid kernel']
clf_linear  = svm.SVC(kernel='linear').fit(x, y)
#clf_linear  = svm.LinearSVC().fit(x, y)
clf_poly    = svm.SVC(kernel='poly', degree=3).fit(x, y)
clf_rbf     = svm.SVC().fit(x, y)
clf_sigmoid = svm.SVC(kernel='sigmoid').fit(x, y)
 
for i, clf in enumerate((clf_linear, clf_poly, clf_rbf, clf_sigmoid)):
    answer = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    print(clf)
    print(np.mean( answer == y_train))
    print(answer)
    print(y_train)
 
    plt.subplot(2, 2, i + 1)
    plt.subplots_adjust(wspace=0.4, hspace=0.4)
    
    # Put the result into a color plot
    z = answer.reshape(xx.shape)
    plt.contourf(xx, yy, z, cmap=plt.cm.Paired, alpha=0.8)
    
    # Plot also the training points
    plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, cmap=plt.cm.Paired)
    plt.xlabel(u'身高')
    plt.ylabel(u'体重')
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    plt.title(titles[i])
    
plt.show()

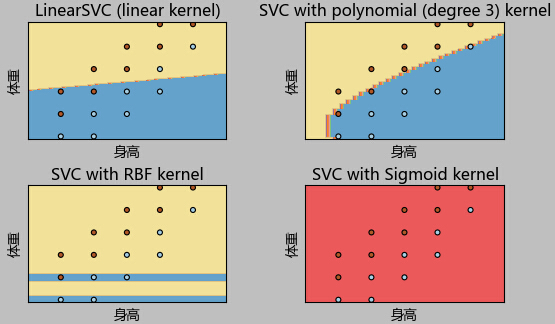
运行结果如下：

可以看到，针对这个数据集，使用3次多项式核函数的SVM，得到的效果最好。

测试2：影评态度

下面看看SVM在康奈尔影评数据集上的表现：（代码略）

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,  kernel='linear', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)
0.814285714286

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,  kernel='poly', max_iter=-1, probability=False, random_state=None,  shrinking=True, tol=0.001, verbose=False)
0.492857142857

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,  kernel='rbf', max_iter=-1, probability=False, random_state=None,  shrinking=True, tol=0.001, verbose=False)
0.492857142857

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,  kernel='sigmoid', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)
0.492857142857
可见在该数据集上，线性分类器效果最好。

测试3：圆形边界

最后我们测试一个数据分类边界为圆形的情况：圆形内为一类，原型外为一类。看这类非线性的数据SVM表现如何：

测试数据生成代码如下所示：

''' 数据生成 '''
h = 0.1
x_min, x_max = -1, 1
y_min, y_max = -1, 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
n = xx.shape[0]*xx.shape[1]
x = np.array([xx.T.reshape(n).T, xx.reshape(n)]).T
y = (x[:,0]*x[:,0] + x[:,1]*x[:,1] < 0.8)
y.reshape(xx.shape)
 
x_train, x_test, y_train, y_test
    = train_test_split(x, y, test_size = 0.2)

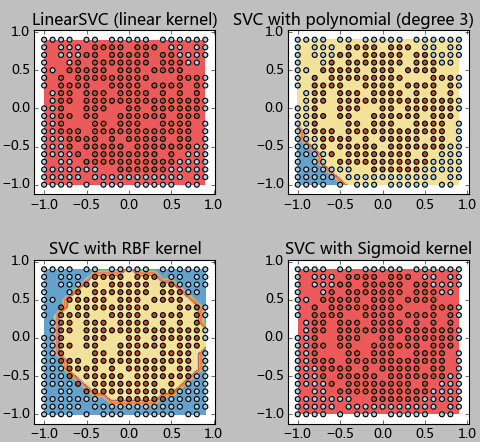
测试结果如下：

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,  kernel='linear', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)
0.65
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,  kernel='poly', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)
0.675
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,  kernel='rbf', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)
0.9625
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,  kernel='sigmoid', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)
0.65

可以看到，对于这种边界，径向基函数的SVM得到了近似完美的分类结果。而其他的分类器显然束手无策。