对于算法思想的理解可以参考下面的这个帖子,十大经典排序算法(动图演示) - 一像素 - 博客园,因为算法的逻辑和数学很像,相应的基础资料一般也能在网上找到,所以,本帖子这谈论一些重要的注意点,其他人讲到的我就不提了,在实现的过程中可能有些代码不是很理解,其他的就相对比较容易多了。
整体按照这个顺序来,也比较好记忆一点:
一、交换排序
1、冒泡排序,基本过程参考前面的帖子,实现代码:
void BubbleSort(int a[], int n) // 本算法将a[]中的元素从小到到大进行排序
{
for(int i = 0; i < n - 1; i++){
flag = false; // 表示本趟冒泡是否发生交换的标志
for(j = n - 1; j > i; j--){ // 一趟冒泡过程
swap(a[j - 1], a[j]); // 为交换函数,将a[j] 与 a[j - 1] 进行交换
flag = true;
}
}
if (flag == false) // 本趟遍历后没有发生交换,说明表已经有序
return;
}
注意:
1)通过设置flag可以直接判断表是否有序,如果有序直接退出,是一个小技巧;
2)排序时间复杂度与表的初始顺序有关,表有序时,比较次数为 n - 1,此为最好的时间复杂度O(n),最差为O(n^2);
3)每趟排序将一个元素放在最终的位置上;
2、快速排序
基于分治法思想,这个与动态图不太一样,针对考研的同学,希望还是以严蔚敏的版本为准:
int partition(int a[], int low, int high){
int pivot = a[low]; // 将当前表中第一个元素设为枢轴值
while(low < high){ // 下标控制条件
while(low < high && a[high] >= pivot)
--high;
a[low] = a[high];
while(low < high && pivot >= a[low])
++low;
a[high] = a[low];
}
a[low] = pivot;
return low; // 返回数组下标,
}
如图,下面的列子:
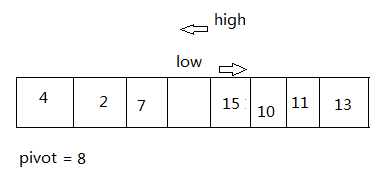
一开始的表 a[ ]
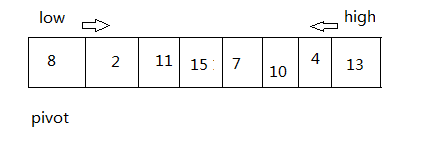
while(low < high && a[high] >= pivot) // 如果a[high]> pivot, high向前移动,直到a[high] < pivot;
--high;
a[low] = a[high]; // 交换
此时的状态:
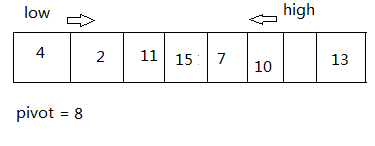
while(low < high && pivot >= a[low]) // 如果a[low] < pivot, low向后移动,直到a[low] > pivot;
++low;
a[high] = a[low]; // 交换
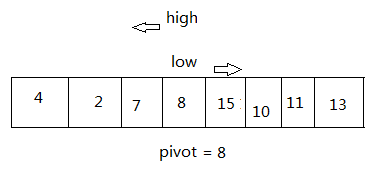
此时的状态:
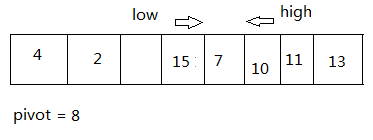
while( low < high) { ... } 的第一遍循环结束,开始第二次的循环:
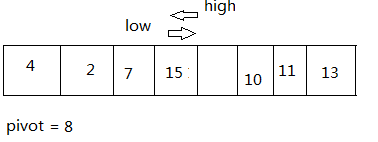
这个小例子比较简单,两遍就结束了,接下来判断条件不满足,退出:
while(low < high){ // 下标控制条件
...
}
a[low] = pivot;
return low; // 返回数组下标,
结果图:
这是各个分支的过程,其中主程序的代码可以采用递归式,也可以采用非递归的,
void QuickSort (int a[], int low, int high){
if (low < high){
int pivot = partition(A, low, high);
QuickSort(A, low, pivot - 1);
QuickSort(A, pivot + 1, high);
} /if
}
point:
1)快排是所有内排序算法平均性能最优的,平均时间复杂度O(nlog₂n),最差为O(n²),平均空间复杂度O(log₂n),最差为O(n);
2)不稳定;
3)其过程中,不产生有序子序列,但是每趟将一个元素放在最终的位置上,就是基准元素;
三、插入排序
1、直接插入排序
这个比较好理解,直接上代码:
void InsertSort(int a[], int n){
int i, j;
for(int i = 2; i <= n; i++){ // 依次将下标2 —— n 插入到已排好的序列
if (a[i] < a[i -1]){ // 前面下标从2开始就是此处 i - 1 的原因
a[0] = a[i]; //
for(j = i -1; a[0] < a[j]; --j){ // 从后面往前查找待插入的元素
a[j + 1] = a[j]; // 向后挪位置
}
a[j + 1] = a[0];
}
}
}
point:
1)移动和比较次数取决于待排序表的初始状态,最好的情况是表已经有序,时间复杂度为O(n), 平均时间复杂度为O(n²);
2)稳定;
3)注意有个哨兵机制,之后的折半插入与希尔排序也是根据此算法转换而来;
2、折半插入排序
基于直接插入排序作出的改动,如图:
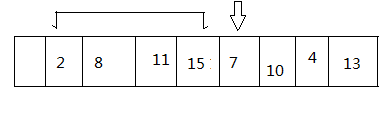
当下边指向7时,前面已经有序,因此利用二分法找到2的后面,然后再直接放入,
point :
1)仅仅是减少了比较的次数,约为O(nlog₂n),该比较次数与待排序表的初始状态无关,仅取决于表中的元素个数n;移动次数没有改变,依赖于待排序表中的初始状态;
2)时间复杂度仍为O(n²)
3)稳定
3、希尔排序
参考的帖子有点小瑕疵,这里面着重提一下:
先上代码:
void ShellSort(int a[], int n){
for(dk = n/2; dk >= 1; dk = df/2){ // 初始增量序列是n/2,后面依次是
for(i = dk+1; i<=n; ++i){
if (a[i] < a[i - dk]){
a[0] = a[i]; // 先暂存在a[0]中
for(j = i-dk; j>0 && a[0]<a[j]; j -= dk){ //j<0 的时候说明到头了
a[j + dk] = a[j];
}
a[j + dk] = a[0]; // 记录后移,查找插入的位置
}
}
}
}
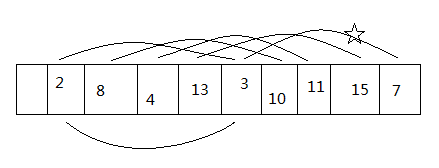
如图,初始数组:

第一趟,dk = n / 2 时,注意,带*号的还没进行比较:
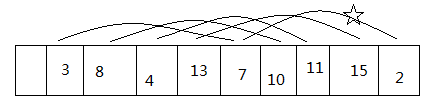
此时,重点来了,
for(j = i-dk; j>0 && a[0]<a[j]; j -= dk){ //j<0 的时候说明到头了 a[j + dk] = a[j];
}
这段代码的作用就是下图的效果,还要与前面同样的增量序列大小进行比较
至此,第一轮循环结束,第二轮增量序列为2 = 4 / 2,之后的过程也是如此,就不重复了。
point:
1)时间复杂度依赖于增量序列的函数,n 取某个值时,最好为O(![]() )
)
2)不稳定