一、什么是分治策略
分治策略是对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。
二、分治法的基本步骤
分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题;
合并:将各个子问题的解合并为原问题的解。
三、典型例题:二分查找,快速排序,归并排序
四、分治策略之棋盘覆盖
一、问题描述
设有n=2^k个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;
(2)每个选手一天只能参赛一次;
(3)循环赛在n-1天内结束。
按此要求将比赛日程表设计成有n行和n-1列的一个表。
在表中的第i行,第j列处填入第i个选手在第j天所遇到的选手。
其中1≤i≤n,1≤j≤n-1。8个选手的比赛日程表如下图:

二、解决思想
按分治策略,我们可以将所有的选手分为两半,则n个选手的比赛日程表可以通过n/2个选手的比赛日程表来决定。递归地用这种一分为二的策略对选手进行划分,直到只剩下两个选手时,比赛日程表的制定就变得很简单。这时只要让这两个选手进行比赛就可以了。
如上图,所列出的正方形表是8个选手的比赛日程表。其中左上角与左下角的两小块分别为选手1至选手4和选手5至选手8前3天的比赛日程。据此,将左上角小块中的所有数字按其相对位置抄到右下角,又将左下角小块中的所有数字按其相对位置抄到右上角,这样我们就分别安排好了选手1至选手4和选手5至选手8在后4天的比赛日程。依此思想容易将这个比赛日程表推广到具有任意多个选手的情形。
三、实现代码
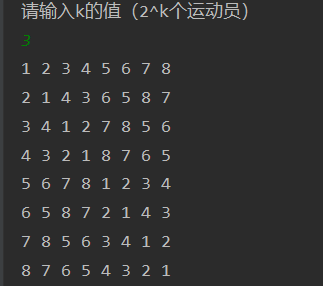
1 package aa; 2 import javax.swing.table.TableCellEditor; 3 import java.lang.annotation.Target; 4 import java.util.Scanner; 5 public class test01 { 6 static int [][]a = new int[100][100]; 7 public static void Table(int k){ //构造循环赛日程表,选手数量n=2的k次; 8 int n = 1<<k; 9 for( int i = 0; i < n; i++ ) 10 a[0][i] = i+1; 11 for( int r = 1; r < n; r = r<<1 ) 12 for( int i = 0; i < n; i = i+r*2 ){ 13 Copy(r,r+i,0,i,r); 14 Copy(r,i,0,r+i,r); 15 } 16 } 17 18 public static void Copy(int tox,int toy,int fromx,int fromy,int r){ 19 for( int i = 0; i < r; i++ ) 20 for( int j = 0; j < r; j++ ){ 21 a[tox+i][toy+j] = a[fromx+i][fromy+j]; 22 } 23 } 24 public static void out(int n){ 25 for(int i = 0;i<n;i++) { 26 for (int j = 0; j < n; j++) { 27 System.out.print(a[i][j] + " "); 28 } 29 System.out.println(); 30 } 31 } 32 33 public static void main(String[] args) { 34 Scanner scanner = new Scanner(System.in); 35 System.out.println("请输入k的值(2^k个运动员)"); 36 int k = scanner.nextInt(); 37 scanner.close(); 38 int n=1<<k; 39 //制作日程表 40 Table(k); 41 //打印日程表 42 out(n); 43 } 44 }
四、执行结果