费马小定理

证明：

由欧拉定理可知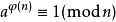      

当gcd(a,n)==1 时 我们有 Aφ(n-1)≡ 1(mod n) ;

所以 我们有 A*Aφ(n-2) ≡ 1(mod n) 

所以Aφ(n-2) 就是A关于mod n的逆元 

#include <iostream>
#include <cstdio>
using namespace std;

int pow(int a,int b,int mod)
{
    int res = 1,base = a;
    while(b!=0){
        if(b&1){
            res *= base % mod;
        }
        base*=base % mod;
        b>>=1;
    }
    return res;
}
int main()
{
    int n,m;
    cin>>n>>m; //n*x=1(mod m) ,求x
    int ans = pow(n,m-2,m);
    cout<<(ans+m)%m<<endl;

    return 0;
}
/*eg:求2关于模13的乘法逆元 2*x=1(mod 13)
通过费马小定理：[前提是13是质数] 2^12=1(mod 13)，
即2^11*2=1(mod 13),2^11即使乘法逆元,用快速冪来求*/

费马小定理推论:

a^p % c=a^(a%(c-1)) %c

如果p可以写成p=k(c-1)+d, 即d=a%(c-1) 
那么, 
a^p %c 
=a^(k(c-1)+d) % c 
=a^(k(c-1))*a^d %c 
=a^(c-1) * …a^(c-1) * a^d % c (…是k个) 
=a^d %c 
所以， 
a^p % c 
=a^(a%(c-1)) %c 

例如这道题：hdu 4704