hdu 2073 无限的路

题目

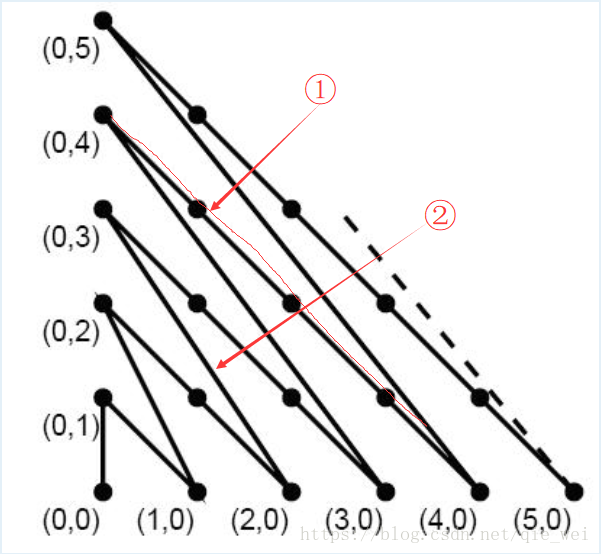
题目是让求两点之间的折线距离，很自然的就可以想到分别求出两点（折线）到原点的距离，然后相减即可，本题没说两点的先后，再多一步取绝对值。
求一点到原点之间的距离，可以把折线分成两部分，一部分是sqrt（2）的整数倍（如图中①所示），另一部分（如图中②所示）

①将两个坐标分开来算长度计算，找到规律，坐标的横纵坐标之和就是最后点所在的线，其中点的纵坐标乘以根号2就是在最后一条线上没走完的距离。

② 第二部分这么求：sqrt（2*2+3*3）,sqrt（3*3+4*4）……

#include <cstdio>
#include <math.h>
double solve(int x,int y)
{
    double dis = 0;
    double tmp = sqrt(2.0);
    for(int i=1;i<=x+y;i++)
        dis += (i*tmp);

    dis -= (y*tmp);
    for(int i=0;i<x+y;i++)
        dis += sqrt((double)i*i+(double)(i+1)*(i+1));
    return dis;
}
int main()
{
    int n,x1,y1,x2,y2;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%.3lf
",fabs(solve(x1,y1)-solve(x2,y2)));
    }
    return 0;
}