1. 极小极大搜索方法
一般应用在博弈搜索中,比如:围棋,五子棋,象棋等。结果有三种可能:胜利、失败和平局。暴力搜索,如果想通过暴力搜索,把最终的结果得到的话,搜索树的深度太大了,机器不能满足,一般都是规定一个搜索的深度,在这个深度范围内进行深度优先搜索。
假设:A和B对弈,轮到A走棋了,那么我们会遍历A的每一个可能走棋方法,然后对于前面A的每一个走棋方法,遍历B的每一个走棋方法,然后接着遍历A的每一个走棋方法,如此下去,直到得到确定的结果或者达到了搜索深度的限制。当达到了搜索深度限制,此时无法判断结局如何,一般都是根据当前局面的形式,给出一个得分,计算得分的方法被称为评价函数,不同游戏的评价函数差别很大,需要很好的设计。
在搜索树中,表示A走棋的节点即为极大节点,表示B走棋的节点为极小节点。
如下图:A为极大节点,B为极小节点。称A为极大节点,是因为A会选择局面评分最大的一个走棋方法,称B为极小节点,是因为B会选择局面评分最小的一个走棋方法,这里的局面评分都是相对于A来说的。这样做就是假设A和B都会选择在有限的搜索深度内,得到的最好的走棋方法。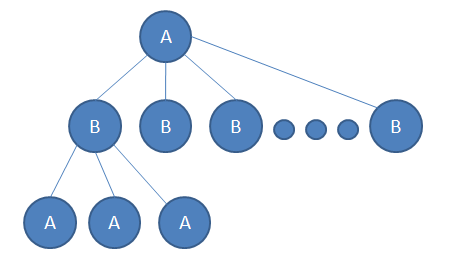
图-极大节点(A)与极小节点(B)
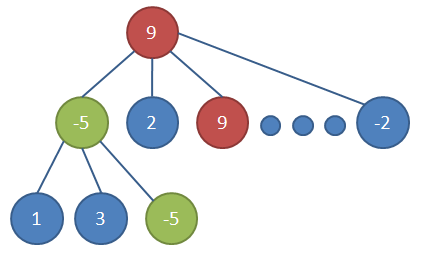
图-极大极小搜索
伪代码如下(来自维基百科):
1 function minimax(node, depth) // 指定当前节点和搜索深度 2 // 如果能得到确定的结果或者深度为零,使用评估函数返回局面得分 3 if node is a terminal node or depth = 0 4 return the heuristic value of node 5 // 如果轮到对手走棋,是极小节点,选择一个得分最小的走法 6 if the adversary is to play at node 7 let α := +∞ 8 foreach child of node 9 α := min(α, minimax(child, depth-1)) 10 // 如果轮到我们走棋,是极大节点,选择一个得分最大的走法 11 else {we are to play at node} 12 let α := -∞ 13 foreach child of node 14 α := max(α, minimax(child, depth-1)) 15 return α;
更加具体一些的算法:
1 int MinMax(int depth) { // 函数的评估都是以白方的角度来评估的 2 if (SideToMove() == WHITE) { // 白方是“最大”者 3 return Max(depth); 4 } else { // 黑方是“最小”者 5 return Min(depth); 6 } 7 } 8 int Max(int depth) { 9 int best = -INFINITY; 10 if (depth <= 0) { 11 return Evaluate(); 12 } 13 GenerateLegalMoves(); 14 while (MovesLeft()) { 15 MakeNextMove(); 16 val = Min(depth - 1); 17 UnmakeMove(); 18 if (val > best) { 19 best = val; 20 } 21 } 22 return best; 23 } 24 int Min(int depth) { 25 int best = INFINITY; // 注意这里不同于“最大”算法 26 if (depth <= 0) { 27 return Evaluate(); 28 } 29 GenerateLegalMoves(); 30 while (MovesLeft()) { 31 MakeNextMove(); 32 val = Max(depth - 1); 33 UnmakeMove(); 34 if (val < best) { // 注意这里不同于“最大”算法 35 best = val; 36 } 37 } 38 return best; 39 }
上面这段代码与前面的伪代码的思路都是一样的,只不过把最大算法和最小算法分为了两个函数。
2. 负值最大算法
前面的两段代码都是分别用两部分代码处理了极大节点和极小节点两种情况,其实,可以只用一部分代码,既处理极大节点也处理极小节点。
不同的是,前面的评估函数是针对白方即,指定的一方来给出分数的,这里的评估函数是根据当前搜索节点来给出分数的。每个人都会选取最大的分数,然后,返回到上一层节点时,会给出分数的相反数。
1 int NegaMax(int depth) { 2 int best = -INFINITY; 3 if (depth <= 0) { 4 return Evaluate(); 5 } 6 GenerateLegalMoves(); 7 while (MovesLeft()) { 8 MakeNextMove(); 9 val = -NegaMax(depth - 1); // 注意这里有个负号 10 UnmakeMove(); 11 if (val > best) { // 都是选择最大的分数,因为评估分数的对象变化了 12 best = val; 13 } 14 } 15 return best; 16 }
这个负值最大算法,主要是代码量上的减少,时间与空间上的效率没有什么提升。
3. Alpha-Beta搜索方法
举例来说,考虑下面的例子:
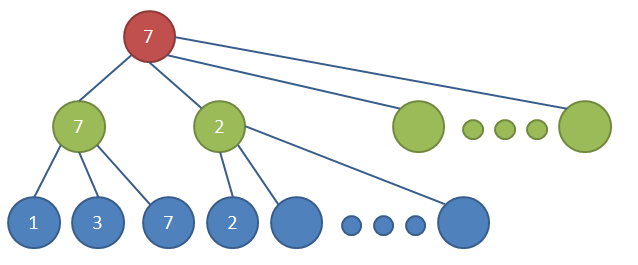
图-alpha-beta搜索
极小极大搜索是一个深度搜索,当搜索到第二层的第二个绿色的节点时,已知其第一个子节点返回值为2,因为这是一个极小节点,那么这个节点得到的值肯定是小于2的,而第二层的第一个绿色节点的值为7,因此这个节点后面即使都搜索了,也不会超过2,更不会超过7,因此这个节点后面的节点可以忽略,即图中第三册没有数字的节点。这属于Alpha剪枝,可能是剪掉的节点是极大节点的原因吧。相应的也有Beta剪枝,图中忽略了。
下面的维基百科伪代码,其中两个值,α表示搜索到的最好的值,β表示搜索到的最坏的值。
1 function alphabeta(node, depth, α, β, Player) 2 if depth = 0 or node is a terminal node 3 return the heuristic value of node 4 if Player = MaxPlayer // 极大节点 5 for each child of node // 极小节点 6 α := max(α, alphabeta(child, depth-1, α, β, not(Player) )) 7 if β ≤ α // 该极大节点的值>=α>=β,该极大节点后面的搜索到的值肯定会大于β,因此不会被其上层的极小节点所选用了。对于根节点,β为正无穷 8 break (* Beta cut-off *) 9 return α 10 else // 极小节点 11 for each child of node // 极大节点 12 β := min(β, alphabeta(child, depth-1, α, β, not(Player) )) // 极小节点 13 if β ≤ α // 该极大节点的值<=β<=α,该极小节点后面的搜索到的值肯定会小于α,因此不会被其上层的极大节点所选用了。对于根节点,α为负无穷 14 break (* Alpha cut-off *) 15 return β 16 (* Initial call *) 17 alphabeta(origin, depth, -infinity, +infinity, MaxPlayer)
4. 参考资料
维基百科-极小化极大算法
最小-最大搜索 http://www.xqbase.com/computer/search_minimax.htm
Alpha-Beta搜索 http://www.xqbase.com/computer/search_alphabeta.htm
原文地址:http://www.cnblogs.com/pangxiaodong/archive/2011/05/26/2058864.html