SimHash算法（转载）

1  SimHash简介

1. 分词，把需要判断文本分词形成这个文章的特征单词，最后形成去掉噪音词的单词序列并为每个词加上权重。我们假设权重分为5个级别（1~5），比如：“ 美国“51区”雇员称内部有9架飞碟，曾看见灰色外星人 ” ==> 分词后为 “ 美国（4） 51区（5） 雇员（3） 称（1） 内部（2） 有（1） 9架（3） 飞碟（5） 曾（1） 看见（3） 灰色（4） 外星人（5）”，括号里是代表单词在整个句子里重要程度，数字越大越重要。
2. hash，通过hash算法把每个词变成hash值，比如“美国”通过hash算法计算为 100101,“51区”通过hash算法计算为 101011。这样我们的字符串就变成了一串串数字，还记得文章开头说过的吗，要把文章变为数字计算才能提高相似度计算性能，现在是降维过程进行时。
3. 加权，通过 2步骤的hash生成结果，需要按照单词的权重形成加权数字串，比如“美国”的hash值为“100101”，通过加权计算为“4 -4 -4 4 -4 4”；“51区”的hash值为“101011”，通过加权计算为 “ 5 -5 5 -5 5 5”。
4. 合并，把上面各个单词算出来的序列值累加，变成只有一个序列串。比如 “美国”的 “4 -4 -4 4 -4 4”，“51区”的 “ 5 -5 5 -5 5 5”， 把每一位进行累加， “4+5 -4+-5 -4+5 4+-5 -4+5 4+5” ==》 “9 -9 1 -1 1 9”。这里作为示例只算了两个单词的，真实计算需要把所有单词的序列串累加。
5. 降维，把4步算出来的 “9 -9 1 -1 1 9” 变成 0 1 串，形成我们最终的simhash签名。 如果每一位大于0 记为 1，小于0 记为 0。最后算出结果为：“1 0 1 0 1 1”。

过程图为：

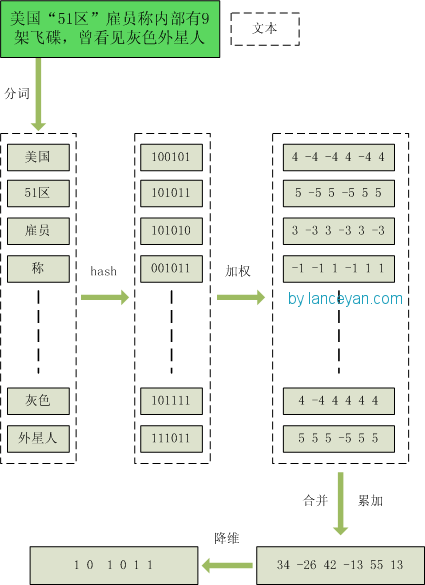
2  算法几何意义及原理

2.1  几何意义

这个算法的几何意义非常明了。它首先将每一个特征映射为f维空间的一个向量，这个映射规则具体是怎样并不重要，只要对很多不同的特征来说，它们对所对应的向量是均匀随机分布的，并且对相同的特征来说对应的向量是唯一的就行。比如一个特征的4位hash签名的二进制表示为1010，那么这个特征对应的 4维向量就是(1, -1, 1, -1)T，即hash签名的某一位为1，映射到的向量的对应位就为1，否则为-1。然后，将一个文档中所包含的各个特征对应的向量加权求和，加权的系数等于该特征的权重。得到的和向量即表征了这个文档，我们可以用向量之间的夹角来衡量对应文档之间的相似度。最后，为了得到一个f位的签名，需要进一步将其压缩，如果和向量的某一维大于0，则最终签名的对应位为1，否则为0。这样的压缩相当于只留下了和向量所在的象限这个信息，而64位的签名可以表示多达264个象限，因此只保存所在象限的信息也足够表征一个文档了。

2.2  原理

明确了算法了几何意义，使这个算法直观上看来是合理的。但是，为何最终得到的签名相近的程度，可以衡量原始文档的相似程度呢？这需要一个清晰的思路和证明。在simhash的发明人Charikar的论文中并没有给出具体的simhash算法和证明，以下列出我自己得出的证明思路。

Simhash是由随机超平面hash算法演变而来的，随机超平面hash算法非常简单，对于一个n维向量v，要得到一个f位的签名(f<<n)，算法如下：

1. 随机产生f个n维的向量r1,…rf；
2. 对每一个向量ri，如果v与ri的点积大于0，则最终签名的第i位为1，否则为0。

这个算法相当于随机产生了f个n维超平面，每个超平面将向量v所在的空间一分为二，v在这个超平面上方则得到一个1，否则得到一个0，然后将得到的 f个0或1组合起来成为一个f维的签名。如果两个向量u, v的夹角为θ，则一个随机超平面将它们分开的概率为θ/π，因此u, v的签名的对应位不同的概率等于θ/π。所以，我们可以用两个向量的签名的不同的对应位的数量，即汉明距离，来衡量这两个向量的差异程度。

Simhash算法与随机超平面hash是怎么联系起来的呢？在simhash算法中，并没有直接产生用于分割空间的随机向量，而是间接产生的：第 k个特征的hash签名的第i位拿出来，如果为0，则改为-1，如果为1则不变，作为第i个随机向量的第k维。由于hash签名是f位的，因此这样能产生 f个随机向量，对应f个随机超平面。下面举个例子：

假设用5个特征w1,…,w5来表示所有文档，现要得到任意文档的一个3维签名。假设这5个特征对应的3维向量分别为：

h(w1) = (1, -1, 1)T

h(w2) = (-1, 1, 1)T

h(w3) = (1, -1, -1)T

h(w4) = (-1, -1, 1)T

h(w5) = (1, 1, -1)T

按simhash算法，要得到一个文档向量d=(w1=1, w2=2, w3=0, w4=3, w5=0) T的签名，

先要计算向量m = 1*h(w1) + 2*h(w2) + 0*h(w3) + 3*h(w4) + 0*h(w5) = (-4, -2, 6) T，然后根据simhash算法的步骤3，得到最终的签名s=001。上面的计算步骤其实相当于，先得到3个5维的向量，第1个向量由h(w1),…,h(w5)的第1维组成：r1=(1,-1,1,-1,1) T；第2个5维向量由h(w1),…,h(w5)的第2维组成：r2=(-1,1,-1,-1,1) T；同理，第3个5维向量为：r3=(1,1,-1,1,-1) T.按随机超平面算法的步骤2，分别求向量d与r1,r2,r3的点积:

d T r1=-4 < 0，所以s1=0;
d T r2=-2 < 0，所以s2=0;
d T r3=6 > 0，所以s3=1.

故最终的签名s=001，与simhash算法产生的结果是一致的。

从上面的计算过程可以看出，simhash算法其实与随机超平面hash算法是相同的，simhash算法得到的两个签名的汉明距离，可以用来衡量原始向量的夹角。这其实是一种降维技术，将高维的向量用较低维度的签名来表征。衡量两个内容相似度，需要计算汉明距离，这对给定签名查找相似内容的应用来说带来了一些计算上的困难。

3  Java算法实现

import java.math.BigInteger;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.StringTokenizer;

public class SimHash {

    private String tokens;

    private BigInteger intSimHash;

    private String strSimHash;

    private int hashbits = 64;

    public SimHash(String tokens) {
        this.tokens = tokens;
        this.intSimHash = this.simHash();
    }

    public SimHash(String tokens, int hashbits) {
        this.tokens = tokens;
        this.hashbits = hashbits;
        this.intSimHash = this.simHash();
    }

    HashMap wordMap = new HashMap();

    public BigInteger simHash() {
        // 定义特征向量/数组
        int[] v = new int[this.hashbits];
        // 1、将文本去掉格式后, 分词.
        StringTokenizer stringTokens = new StringTokenizer(this.tokens);
        while (stringTokens.hasMoreTokens()) {
            String temp = stringTokens.nextToken();
            // 2、将每一个分词hash为一组固定长度的数列.比如 64bit 的一个整数.
            BigInteger t = this.hash(temp);
            for (int i = 0; i < this.hashbits; i++) {
                BigInteger bitmask = new BigInteger("1").shiftLeft(i);
                // 3、建立一个长度为64的整数数组(假设要生成64位的数字指纹,也可以是其它数字),
                // 对每一个分词hash后的数列进行判断,如果是1000...1,那么数组的第一位和末尾一位加1,
                // 中间的62位减一,也就是说,逢1加1,逢0减1.一直到把所有的分词hash数列全部判断完毕.
                if (t.and(bitmask).signum() != 0) {
                    // 这里是计算整个文档的所有特征的向量和
                    // 这里实际使用中需要 +- 权重，而不是简单的 +1/-1，
                    v[i] += 1;
                } else {
                    v[i] -= 1;
                }
            }
        }
        BigInteger fingerprint = new BigInteger("0");
        StringBuffer simHashBuffer = new StringBuffer();
        for (int i = 0; i < this.hashbits; i++) {
            // 4、最后对数组进行判断,大于0的记为1,小于等于0的记为0,得到一个 64bit 的数字指纹/签名.
            if (v[i] >= 0) {
                fingerprint = fingerprint.add(new BigInteger("1").shiftLeft(i));
                simHashBuffer.append("1");
            } else {
                simHashBuffer.append("0");
            }
        }
        this.strSimHash = simHashBuffer.toString();
        System.out.println(this.strSimHash + " length " + this.strSimHash.length());
        return fingerprint;
    }

    private BigInteger hash(String source) {
        if (source == null || source.length() == 0) {
            return new BigInteger("0");
        } else {
            char[] sourceArray = source.toCharArray();
            BigInteger x = BigInteger.valueOf(((long) sourceArray[0]) << 7);
            BigInteger m = new BigInteger("1000003");
            BigInteger mask = new BigInteger("2").pow(this.hashbits).subtract(new BigInteger("1"));
            for (char item : sourceArray) {
                BigInteger temp = BigInteger.valueOf((long) item);
                x = x.multiply(m).xor(temp).and(mask);
            }
            x = x.xor(new BigInteger(String.valueOf(source.length())));
            if (x.equals(new BigInteger("-1"))) {
                x = new BigInteger("-2");
            }
            return x;
        }
    }

    public int hammingDistance(SimHash other) {

        BigInteger x = this.intSimHash.xor(other.intSimHash);
        int tot = 0;

        // 统计x中二进制位数为1的个数
        // 我们想想，一个二进制数减去1，
        //那么，从最后那个1（包括那个1）后面的数字全都反了，
        //对吧，然后，n&(n-1)就相当于把后面的数字清0，
        // 我们看n能做多少次这样的操作就OK了。

        while (x.signum() != 0) {
            tot += 1;
            x = x.and(x.subtract(new BigInteger("1")));
        }
        return tot;
    }

    public int getDistance(String str1, String str2) {
        int distance;
        if (str1.length() != str2.length()) {
            distance = -1;
        } else {
            distance = 0;
            for (int i = 0; i < str1.length(); i++) {
                if (str1.charAt(i) != str2.charAt(i)) {
                    distance++;
                }
            }
        }
        return distance;
    }

    public List subByDistance(SimHash simHash, int distance) {
        // 分成几组来检查
        int numEach = this.hashbits / (distance + 1);
        List characters = new ArrayList();

        StringBuffer buffer = new StringBuffer();

        int k = 0;
        for (int i = 0; i < this.intSimHash.bitLength(); i++) {
            // 当且仅当设置了指定的位时，返回 true
            boolean sr = simHash.intSimHash.testBit(i);

            if (sr) {
                buffer.append("1");
            } else {
                buffer.append("0");
            }

            if ((i + 1) % numEach == 0) {
                // 将二进制转为BigInteger
                BigInteger eachValue = new BigInteger(buffer.toString(), 2);
                System.out.println("----" + eachValue);
                buffer.delete(0, buffer.length());
                characters.add(eachValue);
            }
        }

        return characters;
    }

    public static void main(String[] args) {
        String s = "小明叫她妈妈吃饭";
        SimHash hash1 = new SimHash(s, 64);
        System.out.println(hash1.intSimHash + "  " + hash1.intSimHash.bitLength());
        //hash1.subByDistance(hash1, 3);

        s = "小明叫她妈妈吃饭";
        SimHash hash2 = new SimHash(s, 64);
        System.out.println(hash2.intSimHash + "  " + hash2.intSimHash.bitCount());
        //hash1.subByDistance(hash2, 3);
        
        s = "小明叫她妈妈";
        SimHash hash3 = new SimHash(s, 64);
        System.out.println(hash3.intSimHash + "  " + hash3.intSimHash.bitCount());
        //hash1.subByDistance(hash3, 4);
        
        System.out.println("============================");
        
        int dis = hash1.getDistance(hash1.strSimHash, hash2.strSimHash);
        System.out.println(hash1.hammingDistance(hash2) + " " + dis);

        int dis2 = hash1.getDistance(hash1.strSimHash, hash3.strSimHash);
        System.out.println(hash1.hammingDistance(hash3) + " " + dis2);
        
        //通过Unicode编码来判断中文
        /*String str = "中国chinese";
        for (int i = 0; i < str.length(); i++) {
            System.out.println(str.substring(i, i + 1).matches("[\u4e00-\u9fbb]+"));
        }*/

    }
}

结果：

4  Python算法实现

#!/usr/bin/python  
# coding=utf-8  
class simhash:
    # 构造函数
    def __init__(self, tokens='', hashbits=128):
        self.hashbits = hashbits
        self.hash = self.simhash(tokens);

        # toString函数

    def __str__(self):
        return str(self.hash)

        # 生成simhash值

    def simhash(self, tokens):
        v = [0] * self.hashbits
        for t in [self._string_hash(x) for x in tokens]:  # t为token的普通hash值
            for i in range(self.hashbits):
                bitmask = 1 << i
                if t & bitmask:
                    v[i] += 1  # 查看当前bit位是否为1,是的话将该位+1
                else:
                    v[i] -= 1  # 否则的话,该位-1
        fingerprint = 0
        for i in range(self.hashbits):
            if v[i] >= 0:
                fingerprint += 1 << i
        return fingerprint  # 整个文档的fingerprint为最终各个位>=0的和

    # 求海明距离
    def hamming_distance(self, other):
        x = (self.hash ^ other.hash) & ((1 << self.hashbits) - 1)
        tot = 0;
        while x:
            tot += 1
            x &= x - 1
        return tot

        # 求相似度

    def similarity(self, other):
        a = float(self.hash)
        b = float(other.hash)
        if a > b:
            return b / a
        else:
            return a / b

        # 针对source生成hash值   (一个可变长度版本的Python的内置散列)

    def _string_hash(self, source):
        if source == "":
            return 0
        else:
            x = ord(source[0]) << 7
            m = 1000003
            mask = 2 ** self.hashbits - 1
            for c in source:
                x = ((x * m) ^ ord(c)) & mask
            x ^= len(source)
            if x == -1:
                x = -2
            return x


if __name__ == '__main__':
    s = '小明叫她妈妈吃饭'
    hash1 = simhash(s.split())

    s = '小明叫她妈妈吃饭'
    hash2 = simhash(s.split())

    s = '小明叫她妈妈'
    hash3 = simhash(s.split())

    print(hash1.hamming_distance(hash2), "   ", hash1.similarity(hash2))
    print(hash1.hamming_distance(hash3), "   ", hash1.similarity(hash3))

结果：

注：SimHash适用于大文本处理（>400字），对于小文本而言，误差较大！！！