红黑树之删除节点
上一篇文章中讲了如何向红黑树中添加节点,也顺便创建了一棵红黑树。今天写写怎样从红黑树中删除节点。
相比于添加节点,删除节点要复杂的多。不过我们慢慢梳理,还是能够弄明白的。
回顾一下红黑树的性质
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶节点(这里的叶节点是指NULL节点,在《算法导论》中这个节点叫哨兵节点,除了颜色属性外,其他属性值都为任意。为了和以前的叶子节点做区分,原来的叶子节点还叫叶子节点,这个节点就叫他NULL节点吧)是黑色的。
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点,或者理解为红节点不能有红孩子)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点(黑节点的数目称为黑高black-height)。
首先先说一下我们要删除节点的类型
我们要删除的节点类型从大的方面来说,只有两种:
1、 单个的叶子节点(不是指NULL节点,就是二叉排序树中的叶子节点的概念)
2、 只有右子树(或只有左子树)的节点
为什么这样呢?
我们知道,对于一棵普通的二叉排序树来说,删除的节点情况可以分为3种:
1、 叶子节点
2、 只有左子树或只有右子树的节点
3、 既有左子树又有右子树的节点。
我们知道对于一棵普通二叉树的情况3来说,要删除既有左子树又有右子树的节点,我们首先要找到该节点的直接后继节点,然后用后继节点替换该节点,最后按1或2中的方法删除后继节点即可。
所以情况3可以转换成情况1或2。
同样,对于红黑树来讲,我们实际上删除的节点情况只有两种。
对于情况2,也就是待删除的节点只有左子树或这有右子树的情况,有很多组合在红黑树中是不可能出现的,因为他们违背了红黑树的性质。
情况2中不存在的情况有(其中D表示要删除的节点,DL和DR分别表示左子和右子):
1、
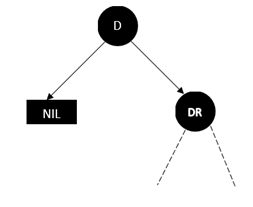
2、
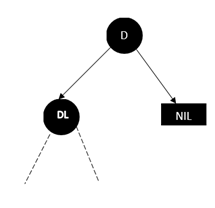
3、
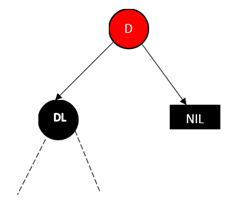
4、
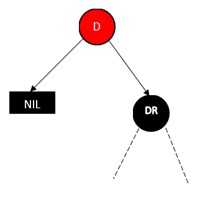
上面这四种明显都违背了性质5
5、
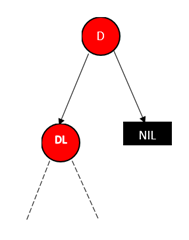
6、
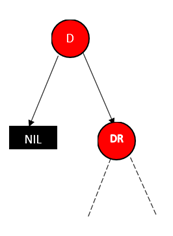
5和6两种情况明显都违背了性质4
此外对于删除红色节点的情况比较简单,我们可以先来看看。
我们上面把待删除的节点分成为了两种,那这里,对于删除的红色节点,我们也分两种:
1、 删除红色的叶子节点(D表示待删除的节点,P表示其父亲节点)
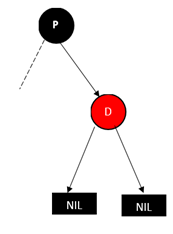
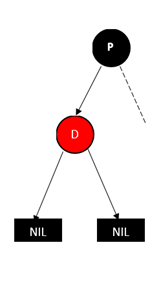
上面这两种情况其实处理方式都一样,直接删除D就好!
2、 删除的红色节点只有左子树或只有右子树
上面已经分析了,红黑树中根本不存在这种情况!!
接下来我们要讨论删除最复杂的情况了,也就是删除的节点为黑色的情况
同样,我们也将其分成两部分来考虑:
1、 删除黑色的叶子节点
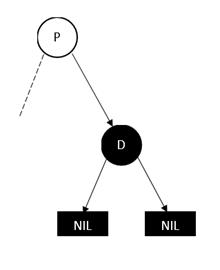
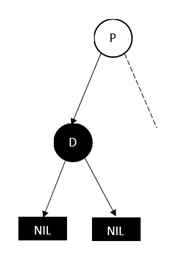
对于这种情况,相对复杂,后面我们再细分
2、 删除的黑色节点仅有左子树或者仅有右子树
去掉前面已经分析的不存在的情况。这种情况下节点的结构只肯能是
(竖直的西线代替了左右分支的情况)
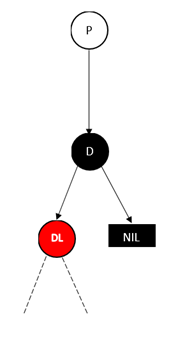
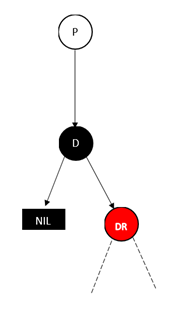
这两种情况的处理方式是一样的,即用D的孩子(左或右)替换D,并将D孩子的颜色改成黑色即可(因为路径上少了一个黑节点,所已将红节点变成黑节点以保持红黑树的性质)。
所以,这些情况处理起来都很简单。。。除了,删除黑色叶子节点的情况。
下面重点讨论删除黑色叶子节点的情况
情况1:待删除节点D的兄弟节点S为红色
D是左节点的情况
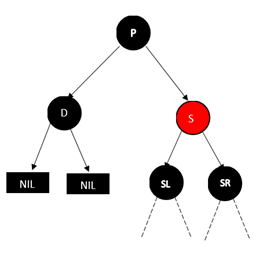
调整做法是将父亲节点和兄弟节点的颜色互换,也就是p变成红色,S变成黑色,然后将P树进行AVL树种的RR型操作,结果如下图
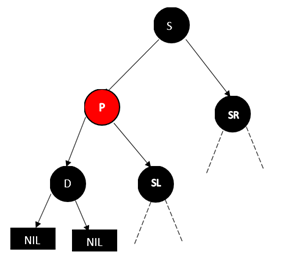
这个时候我们会发现,D的兄弟节点变成了黑色,这样就成后面要讨论的情况。
D是右节点的情况
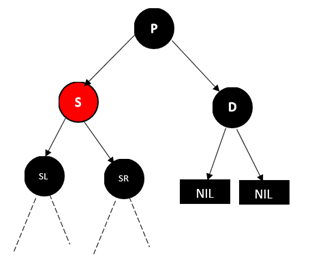
将P和S的颜色互换,也就是将P变成红色,将S变成黑色,然后对P进行类似AVL树的LL操作。结果如下图:
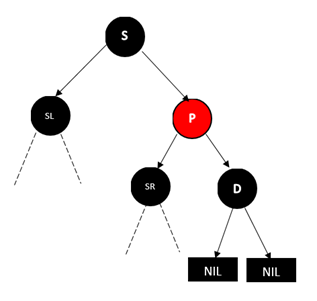
此时D的兄弟节点变成了黑色,这样就成了我们后面要讨论的情况
情况2:兄弟节点为黑色,且远侄子节点为红色。
D为左孩子对的情况,这时D的远侄子节点为S的右孩子
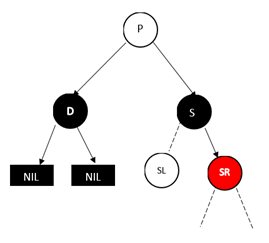
没有上色的节点表示黑色红色均可,注意如果SL为黑色,则SL必为NULL节点。
这个时候,如果我们删除D,这样经过D的子节点(NULL节点)的路径的黑色节点个数就会减1,但是我们看到S的孩子中有红色的节点,如果我们能把这棵红色的节点移动到左侧,并把它改成黑色,那么就满足要求了,这也是为什么P的颜色无关,因为调整过程只在P整棵子树的内部进行。
调整过程为,将P和S的颜色对调,然后对P树进行类似AVL树RR型的操作,最后把SR节点变成黑色,并删除D即可。
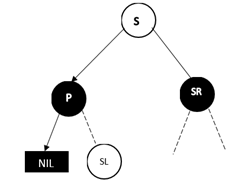
D为右孩子的情况,此时D的远侄子为S的左孩子
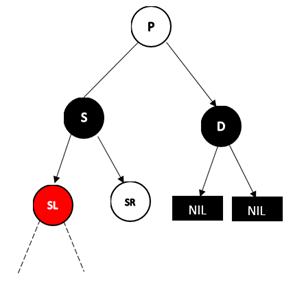
同样,将P和S的颜色对调,然后再对P树进行类似AVL树RL型的操作,最后将SR变成黑色,并删掉D即可。结果如下图:
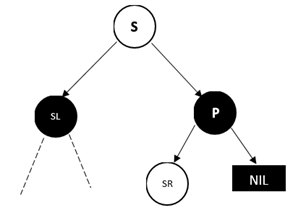
情况3:兄弟节点S为黑色,远侄子节点为黑色,近侄子节点为红色
D为左孩子的情况,此时近侄子节点为S的左孩子

做法是,将SL右旋,并将S和SL的颜色互换,这个时候就变成了情况4。
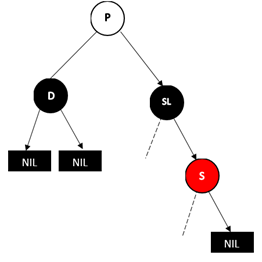
D为右孩子的情况,此时近侄子节点为S的右孩子
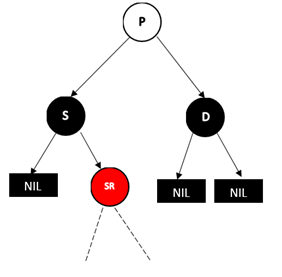
做法是将S和SR颜色对调,然后对SR进行左旋操作,这样就变成了情况4,结果如下图:
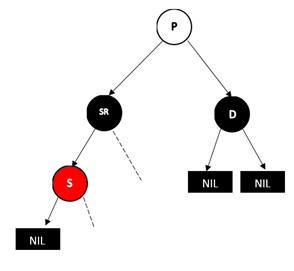
情况4:父亲节p为红色,兄弟节点和兄弟节点的两个孩子(只能是NULL节点)都为黑色的情况。
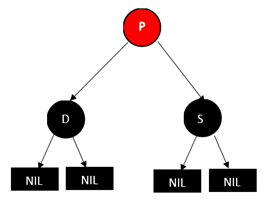
如果删除D,那经过P到D的子节点NULL的路径上黑色就少了一个,这个时候我们可以把P变成黑色,这样删除D后经过D子节点(NULL节点)路径上的黑色节点就和原来一样了。但是这样会导致经过S的子节点(NULL节点)的路径上的黑色节点数增加一个,所以这个时候可以再将S节点变成红色,这样路径上的黑色节点数就和原来一样啦!
所以做法是,将父亲节点P改成黑色,将兄弟节点S改成红色,然后删除D即可。如下图:
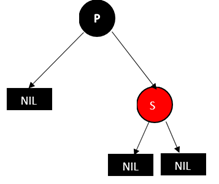
情况5:父亲节点p,兄弟节点s和兄弟节点的两个孩子(只能为NULL节点)都为黑色的情况
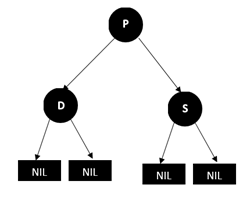
方法是将兄弟节点S的颜色改成红色,这样删除D后P的左右两支的黑节点数就相等了,但是经过P的路径上的黑色节点数会少1,这个时候,我们再以P为起始点,继续根据情况进行平衡操作(这句话的意思就是把P当成D(只是不要再删除P了),再看是那种情况,再进行对应的调整,这样一直向上,直到新的起始点为根节点)。结果如下图:
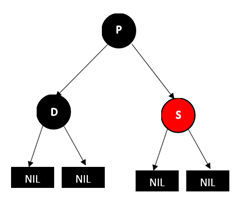
至此,所有的情况都讨论完了。我们稍稍总结一下,然后开始时写代码
我这里总结的是如何判断是那种类型,至于特定类型的处理方法,就找前面的内容就好。
记住一句话:判断类型的时候,先看待删除的节点的颜色,再看兄弟节点的颜色,再看侄子节点的颜色(侄子节点先看远侄子再看近侄子),最后看父亲节点的颜色。把握好这一点,写代码思路就清晰了。
流程图如下(忽略了处理过程)
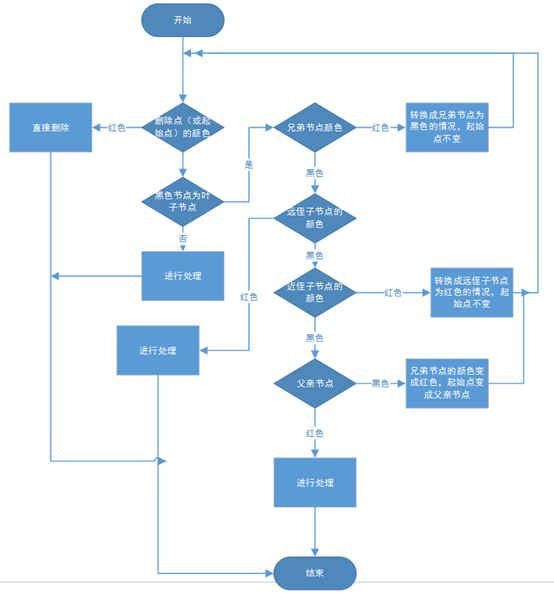
开始写代码啦
节点的数据结构
//定义节点的颜色 enum color{ BLACK, RED }; //节点的数据结构 typedef struct b_node{ int value;//节点的值 enum color color;//树的深度 struct b_node *l_tree;//左子树 struct b_node *r_tree;//右子树 struct b_node *parent;//父亲节点 } BNode,*PBNode; /** * 分配一个节点 * */ PBNode allocate_node() { PBNode node = NULL; node = (PBNode)malloc(sizeof(struct b_node)); if(node == NULL) return NULL; memset(node,0,sizeof(struct b_node)); return node; } /** * 设置一个节点的值 * */ void set_value(PBNode node,int value) { if(node == NULL) return; node->value = value; node->color = RED; node->l_tree = NULL; node->r_tree = NULL; node->parent = NULL; } 释放节点空间的函数 /** * 释放节点空间 * */ void free_node(PBNode *node) { if(*node == NULL) return; free(*node); *node = NULL; }
后面是与删除有关的函数,我们由易到难,先小后大进行处理。
首先,我们先写一个删除节点的函数:
/** * 删除一个节点 * 其中root为整棵树的根结点 * d为待删除的节点,或者新的起始点 * */ void delete_node(PBNode *root,PBNode d) { PBNode p = d->parent;//父亲节点 if(p == NULL)//说明d就是树根 { free_node(root); return; } if(p->l_tree == d) p->l_tree = NULL; else if(p->r_tree == d) p->r_tree = NULL; free_node(&d); }
删除红色节点的情况非常简单,只需要删除节点就行,所以直接调用删除函数即可。
/** * 删除红色节点 * */ void delete_d_red(PBNode *root,PBNode d) { delete_node(root,d); } 删除黑色节点的情况比较复杂,我们先处理小的模块: 黑色节点非叶子节点 /** * 黑色节点不是叶子节点,这时候它只有一个孩子,且孩子的颜色为红色 * * */ void delete_d_black_not_leaf(PBNode *root,PBNode d) { PBNode dl_r; if(d->l_tree != NULL) { dl_r = d->l_tree; } else if(d->r_tree != NULL) { dl_r = d->r_tree; } else { printf("节点有问题! "); return; } dl_r->color = BLACK; PBNode p = d->parent;//父亲节点 if(p == NULL)//说明是整棵树的树根 { *root = dl_r; } else { if(p->l_tree == d) { p->l_tree = dl_r; } else if(p->r_tree == d) { p->r_tree = dl_r; } } //别忘了修改父亲节点 dl_r->parent = p; free_node(&d); }
删除黑色叶子节点是最复杂的一种情况,这种情况总体要再循环中进行,循环结束条件为:新的起始节点为根节点。当然,如果循环中某种类型变换完成后,可以确定整棵树都满足红黑树,循环也就结束了。
D为叶子节点且兄弟节点为红色的情况(也就是情况1):
这种情况涉及RR型变换和RL型变换,所以我们先写一个函数用来处理RR型和RL型变换。
/** * RR类型和LL类型的变换 * */ void avl_trans(PBNode *root,PBNode ch_root,enum unbalance_type type) { int t = type; PBNode small; PBNode middle; PBNode big; switch (t) { case TYPE_LL: { //确定small、middle、big三个节点 big = ch_root; middle = ch_root->l_tree; small = ch_root->l_tree->l_tree; //分配middle节点的孩子,给small和big big->l_tree = middle->r_tree; //别忘了该父亲节点!!!!!!!!! if(middle->r_tree != NULL) middle->r_tree->parent = big; //将small和big作为midlle的左子和右子 middle->r_tree = big; break; } case TYPE_RR: { //确定small、middle、big三个节点 small =ch_root; middle = ch_root->r_tree; big = ch_root->r_tree->r_tree; //分配middle节点的孩子,给small和big small->r_tree = middle->l_tree; //别忘了该父亲节点!!!!!!!!! if(middle->l_tree != NULL) middle->l_tree->parent = small; //将small和big作为midlle的左子和右子 middle->l_tree = small; break; } } //将子树的父亲节点的子节点指向middle(也就是将middle,调整后的子树的根结点) if(ch_root->parent == NULL) //说明子树的根节点就是整棵树的根结点 { *root = middle; } else if(ch_root->parent->l_tree == ch_root)//根是父亲的左孩子 { ch_root->parent->l_tree = middle; } else if(ch_root->parent->r_tree == ch_root)//根是父亲的右孩子 { ch_root->parent->r_tree = middle; } //更改small、middle、big的父亲节点 middle->parent = ch_root->parent; big->parent = middle; small->parent = middle; }
有了这两个变换的函数后,对于兄弟节点为红色的这种情况,处理起来就很简单了。
/** * D为黑色,S为红色的情况 * 也就是情况1 * 将其类型变换成D为黑色,S也为黑色的情况 * */ void delete_black_case1(PBNode *root,PBNode d) { PBNode p = d->parent;//父亲节点 if(p->l_tree == d)//d为左子的情况 { PBNode s = p->r_tree; p->color = RED;//父亲节点变成红色 s->color = BLACK;//兄弟节点变成黑色 avl_trans(root,p,TYPE_RR); } else if(p->r_tree == d)//d为右子的情况 { PBNode s = p->l_tree; p->color = RED;//父亲节点变成红色 s->color = BLACK;//兄弟节点变成黑色 avl_trans(root,p,TYPE_LL); } }
S为黑色,远侄子节点为红色的情况(也就是情况2):
/** * D为黑色,S为黑色,远侄子节点为红色 * 也就是情况2 * */ void delete_black_case2(PBNode *root,PBNode d) { PBNode p = d->parent;//父亲节点 if(p->l_tree == d)//d为左孩子的情况 { PBNode s = p->r_tree;//兄弟节点 //交换父亲姐弟和兄弟节点的颜色 enum color temp = p->color; p->color = s->color; s->color = temp; PBNode far_nephew = s->r_tree;//远侄子节点 far_nephew->color = BLACK;//将远侄子节点的颜色变成黑色 avl_trans(root,p,TYPE_RR);//进行类似AVL树RR类型的转换 } else if(p->r_tree == d)//d为右孩子的情况o { PBNode s = p->l_tree;//兄弟节点 //交换父亲姐弟和兄弟节点的颜色 enum color temp = p->color; p->color = s->color; s->color = temp; PBNode far_nephew = s->l_tree;//远侄子节点 far_nephew->color = BLACK;//将远侄子节点的颜色变成黑色 avl_trans(root,p,TYPE_LL);//进行类似AVL树LL类型的转换 } }
D为黑色,S为黑色,远侄子为黑色,近侄子为红色的情况(也就是情况3)
这种情况涉及节点的左旋和右旋操作,所以写一个函数处理节点的旋转
/** * 处理左旋和右旋操作 * */ void node_rotate(PBNode to_rotate,enum rotate_type type) { PBNode p = to_rotate->parent;//父亲节点 PBNode g = p->parent;//祖父节点 int t = type; switch(t) { case TURN_RIGHT: { g->r_tree = to_rotate; p->l_tree = to_rotate->r_tree; to_rotate->r_tree = p; break; } case TURN_LEFT: { g->l_tree = to_rotate; p->r_tree = to_rotate->l_tree; to_rotate->l_tree = p; break; } } //别忘了更改父亲节点 to_rotate->parent = g; p->parent = to_rotate; }
有了旋转操作,剩下的就只有颜色变换了。
/** * D为黑色,S为黑色,远侄子为黑色,近侄子为红色 * 也就是情况3 * 通过旋转近侄子节点,和相关颜色变换,使情况3变成情况2 * */ void delete_black_case3(PBNode d) { PBNode p = d->parent;//父亲节点 if(p->l_tree == d)//d为左孩子的情况 { PBNode s = p->r_tree; PBNode near_nephew = s->l_tree; s->color = RED; near_nephew->color = BLACK; node_rotate(near_nephew,TURN_RIGHT); } else if(p->r_tree == d) { PBNode s = p->l_tree; PBNode near_nephew = s->r_tree; s->color = RED; near_nephew->color = BLACK; node_rotate(near_nephew,TURN_LEFT); } }
父亲节p为红色,兄弟节点和兄弟节点的两个孩子(只能是NULL节点)都为黑色的情况,也就是情况4
这种情况比较简单,只涉及颜色的改变
/** * D为黑色,S为黑色,远侄子为黑色,近侄子为黑色,父亲为红色 * 也就是情况4 * */ void delete_black_case4(PBNode d) { PBNode p = d->parent;//父亲节点 if(p->l_tree == d)//d为左孩子 { PBNode s = p->r_tree; s->color = RED; } else if(p->r_tree == d)//d为左孩子 { PBNode s = p->l_tree; s->color = RED; } p->color = BLACK; }
父亲节点p,兄弟节点s和兄弟节点的两个孩子(只能为NULL节点)都为黑色的情况,也就是情况5
这种情况也比较简单,就是将S的颜色变成红色,将起始点有d变成p即可
/** * D,S,P,SL,SR都为黑色的情况 * 也就是情况5 * */ PBNode delete_black_case5(PBNode d) { PBNode p = d->parent;//父亲节点 if(p->l_tree == d)//d为左孩子 { PBNode s = p->r_tree; s->color = RED; } if(p->r_tree == d)//d为左孩子 { PBNode s = p->l_tree; s->color = RED; } return p; }
最后要写一个串联函数,将删除黑色叶子节点的各个函数串联起来,这个串联函数中有循环,循环结束条件是新的起始点为根节点,但是由于情况1-4,处理结束后,整棵树就是红黑树了,此时可以用break退出循环。
/** * 删除黑色叶子节点的函数,会将上面的多个函数串连起来 * */ void delete_d_black_leaf(PBNode *root,PBNode d) { PBNode begin = d;//起始节点 while(begin != *root) { PBNode p = begin->parent;//父亲节点 if(p->l_tree == begin)//d为左孩子 { PBNode s = p->r_tree;//兄弟节点 if(s->color == RED)//情况1 { delete_black_case1(root,begin); continue; } PBNode sl = s->l_tree;//近侄子 PBNode sr = s->r_tree;//远侄子 if(sr != NULL && sr->color == RED)//情况2 { delete_black_case2(root,begin); break; } if(sl != NULL && sl->color == RED)//情况3 { delete_black_case3(begin); continue; } if(p->color == RED)//情况4 { delete_black_case4(begin); break; } //情况5 begin = delete_black_case5(begin);//起始点要变换 continue; } else if(p->r_tree == begin)//d为左孩子 { PBNode s = p->l_tree;//兄弟节点 if(s->color == RED)//情况1 { delete_black_case1(root,begin); continue; } PBNode sl = s->l_tree;//远侄子 PBNode sr = s->r_tree;//近侄子 //一定要先看远侄子,再看近侄子 if(sl != NULL && sl->color == RED)//情况2 { delete_black_case2(root,begin); break; } if(sr != NULL && sr->color == RED)//情况3 { delete_black_case3(begin); continue; } if(p->color == RED)//情况4 { delete_black_case4(begin); break; } //情况5 begin = delete_black_case5(begin);//起始点要变换 continue; } } //循环退出后,删除d delete_node(root,d); }
最后写一个函数将删除红色节点、黑色非叶子节点和黑色叶子节点的函数合并到一起,此外还要根据二叉排序树的要求处理有两个孩子的节点
/** * 删除节点函数,并进行调整,保证调整后任是一棵红黑树 * */ void delete_brt_node(PBNode *root,int value) { //找到该节点 PBNode node = get_node(*root,value); if(node == NULL) return; int tag = 0; while(tag != 2) { if(node->l_tree == NULL) { PBNode r = node->r_tree; if(r == NULL)//为叶子节点的情况 { if(node->color == RED) { delete_d_red(root,node); } else { delete_d_black_leaf(root,node); } break; } else//只有右子树的情况 { delete_d_black_not_leaf(root,node); break; } } else if(node->r_tree == NULL)//只有左子树的情况 { delete_d_black_not_leaf(root,node); break; } else//既有左孩子又有右孩子 { //找到后继节点 PBNode y = node->r_tree; while(y->l_tree != NULL) { y = y->l_tree; } //用后继节点和该节点进行值交换 int temp = node->value; node->value = y->value; y->value = temp; node = y;//待删除的节点转换成后继节点 tag ++; } } }
最后附上word文档和源代码文件
链接:http://pan.baidu.com/s/1nvQI2iX 密码:16nd
那个brt2.c是包含添加和删除节点的
如果你觉得对你有用,请点个赞吧~~~光图都画了好长时间~~