参考资料:《信号与系统(第二版)》 杨晓非 何丰
信号的描述
施加于系统的信号叫做输入信号或者激励,系统产生的信号叫做系统的输出信号或者响应。
信号的时间特性:信号可以描绘成随时间变化的波形图,信号在某一时刻的大小,信号持续时间的长短,信号变化的快慢等都可以在波形图上反应出来的特性。
信号的频率特性:信号在一定条件下可以分解成不同频率的正弦分量之和,正弦分量的振幅和初相位,频率之间的关系反映出来的特性。
信号的分类
确定信号:信号可以写出一个确定的时间函数表达式,对于每一时刻t都有确定的函数值与其对应。
随机信号:信号不能写出确定时间的函数表达式,只能用概率统计的方法来描述,只能预测某一个时刻为一个值的概率,但是该时刻的具体数值是未知的。
连续时间信号(简称连续信号):除了有限的间断点之外,如果一个信号在任意时刻均有定义值,那么该信号称为连续信号。时间自变量t必须是连续变化的,函数值可允许个别时刻跳变,如果信号的时间自变量和函数值均是连续变化的,则称为模拟信号。
离散信号:只在一系列离散的瞬间有确切定义而在其他时刻无定义的信号叫做离散时间信号,离散信号可以对连续信号以等间隔时间T进行取样得到,其自变量是离散时间KT,而不是连续时间t。
取样信号:时间离散而函数取值连续的信号。
如何理解这里的时间离散但函数取值连续呢??
通过对连续信号进行等间隔时间取样,可以知道所谓的时间离散指的是时间单位是可以量化的,也就是等间隔的,离散的。函数取值并不是等间隔的,幅值可能有无限多个值,因此不是离散的,而是连续的。如果我们现在对函数值以0,1,2,3,4,5,6...进行量化,量化后的值取决于函数值与0,1,2,3,4,5,6...的接近程度,那么量化之后,所有的函数值都变成离散的了,当一个取样信号时间和函数取值均为离散的时候,这样的信号称为数字信号。
周期信号:按照一定的时间周期T周而复始地重复出现并且时间域是无始无终的信号。
因果信号:输出仅与当前或之前的输入有关的信号。
通俗理解因果信号(causal system)
当系统的输出仅与当前的输入或者过去的输入有关,那么这个系统就是causal的。换句话说,如果一个系统和未来的输入有关,那就不是causal的。 举三个例子,都把我的身体看做一个系统,把一杯咖啡看做输入,期待的输出是兴奋状态。现在我喝了一杯咖啡,30 min 后我的身体开始变得兴奋,这就是causal的。现在一杯热咖啡被打翻了,我被它烫到的瞬间我就觉得疼了,这也是causal的。如果我现在喝一杯喝咖啡是为了让我两小时之前兴奋起来(或者说我现在的兴奋依赖于未来的一杯咖啡),那就不causal了。 现实中,一个系统如果不causal,就像最后这个例子这样让人感觉怪异,恐怕没法实现。
在数学表达上,x(t)是当前的输入,x(t - 1)是n个时间单位之前的输入,x(t + 1)是n个时间单位之后的输入。所以如果你看到 y(t) = x(t + 1),就知道它再说:当前的输出y(t)等于未来的一个输入,这就属于不causal。对于任意的一个提前量或者推迟量,用n表示,一个输入可以写成x(t + n)的形式。当n分别小于零、等于零、大于零的时候,分别对应着过去、当前、未来的输入。
举个例子,以助于理解causal system。当假设x(t) 作用于 t = 0 之后,那么一个causal system 产生响应的时间点必然晚于 0 点,即 t >= 0 ,在这之前响应都是 0 。
典型信号
1.连续信号
- 单位斜坡信号
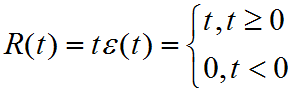
锯齿形脉冲信号和正三角脉冲信号都是单位斜坡信号的变形
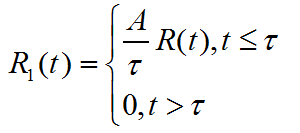
- 单位阶跃信号
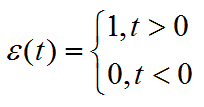
单位阶跃信号ε(t)的定义可以理解为:
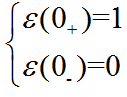
t<0甚至t=0-时,ε(t)=0;t>0甚至t=0+时,ε(t)=1,当0-<t<0+时,ε(t)在0和1之间处于一种不确定的状态。
单位门函数 gτ(t)=ε(t+τ/2)-ε(t-τ/2),用单位阶跃信号来表示,幅值为1。
单位阶跃信号是单位斜变信号的导数,单位斜变信号是单位阶跃信号的积分。
- 单位冲激信号
单位冲激信号δ(t)又叫单位冲激函数。
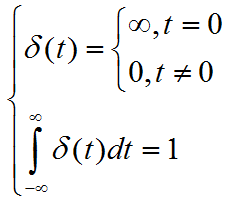
该定义有三层含义:
- δ(t)仅在t=0瞬间有一个幅度为无穷大的“冲激”
- t!=0的时间里δ(t)函数值处处为0
- δ(t)在全时域积分为1,它与时间轴构成的面积为1,该积分称为冲激函数的强度。
Aδ(t)表示强度为A的冲激信号。
冲激函数的其他函数表示:
- 门限函数表示
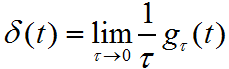
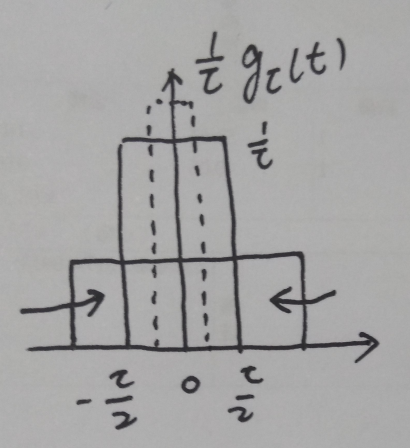
根据冲激函数的定义在0处的幅值为无穷大,全时域的积分为1,也就是面积为1,实际上就是构造函数。单位门函数 gτ(t)=ε(t+τ/2)-ε(t-τ/2),用单位阶跃信号来表示,幅值为1,面积为τ,因此要幅值要变成1/τ.
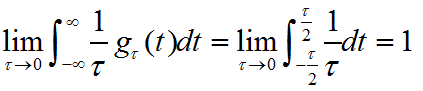
冲激函数的性质:
- 加权性质 (前提条件:f(t)在t=0的时候连续)
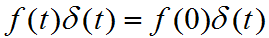
连续信号与冲激信号的乘积,在时间t=0时等于一个强度为f(0)的冲激函数f(0)δ(t),其余时间(t != 0)的时候均为0
推论:若函数在t=t0连续
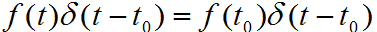
当δ(t)不为0的时候才有值,因此t=t0
- 取样性质(前提条件:f(t)在t=0的时候连续)
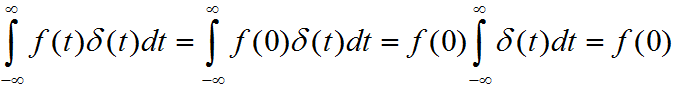
- 偶函数性质
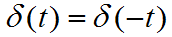
- 尺度变换性质
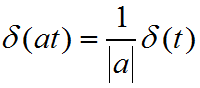
推论: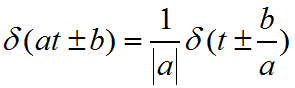
- δ(t)和ε(t)的关系
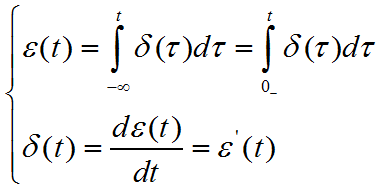
2.离散信号