Dijkstra算法的使用条件:图中不存在负权边。
---------------------------有待验证------------------------
Dijkstra 算法,用于对有权图进行搜索,找出图中两点的最短距离,既不是DFS搜索,也不是BFS搜索。
把Dijkstra 算法应用于无权图,或者所有边的权都相等的图,Dijkstra 算法等同于BFS搜索。
--------------------------------------------------------------
算法思想描述:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点之间的距离,是从v到此顶点(只包括S中的顶点为中间顶点)的当前最短路径长度。
注意:对算法思想描述中的加粗字体的理解非常重要,后面会在有权图的最短路径求解步骤中给出理由和陷阱。
原博客中有图和步骤表格,这里不再进行复制,有兴趣的同学可以移步文章开头链接,这里重新用另外一张图进行说明
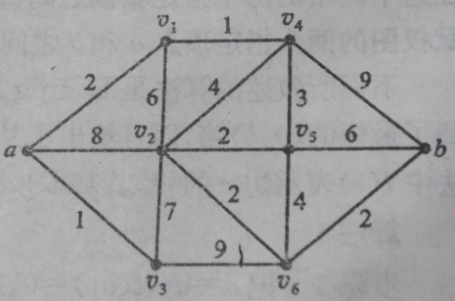
| 步骤 | S集合 | U集合 |
|
1 |
选入a,此时S=<a> 此时最短路径a→a=0 以a为中间点,从a开始找 |
U=<v1、v2、v3、v4、v5、v6、b> a→v1=2 a→v2=8 a→v3=1 a→其他U中的顶点=∞ 发现a→v3=1权值最短 |
|
2 |
选入v3,此时S=<a、v3> 此时最短路径a→a=0,a→v3=1 以v3为中间点,从a→v3=1这条最短路径开始找 |
U=<v1、v2、v4、v5、v6、b> a→v3→v2=8(比上面第一步的a→v2=8相等,保持不变) a→v3→v6=10 a→v3→其他U中的顶点=∞(这里有a→v3→v1=∞, 比第一步中的a→v1=2要长),此时a到v1的权值更改为a→v1=2 发现a→v1=2权值最短 |
| 3 | 选入v1,此时S=<a、v3、v1>
此时最短路径a→a=0,a→v3=1,a→v1=2 以v1为中间点,从a→v1=2这条最短路径开始找 |
U=<v2、v4、v5、v6、b> a→v1→v2=8(比上面第一步的a→v2=8相等,保持不变) a→v1→v4=3 a→v1→其他U中的顶点=∞ 发现a→v1→v4=3权值最短 |
| 4 |
选入v4,此时S=<a、v3、v1、v4> 此时最短路径a→a=0,a→v3=1,a→v1=2, a→v1→v4=3 以v4为中间点,从a→v1→v4=3这条最短路径开始找 |
U=<v2、v5、v6、b> a→v1→v4→v2=7(比上面第一步的a→v2=8要短) 此时a到v2的权值更改为a→v1→v4→v2=7 a→v1→v4→v5=6 a→v1→v4→b=12 a→v1→v4→其他U中的顶点=∞ 发现a→v1→v4→v5=6权值最短 |
| 5 |
选入v5,此时S=<a、v3、v1、v4、v5> 此时最短路径 a→a=0,a→v3=1,a→v1=2, a→v1→v4=3,a→v1→v4→v5=6 以v5为中间点,从a→v1→v4→v5=6这条最短路径 开始找 |
U=<v2、v6、b> a→v1→v4→v5→v2=8(比上面第四步的a→v1→v4→v2=7要长) 此时a到v2的权值更改为a→v1→v4→v2=7 a→v1→v4→v5→v6=10 a→v1→v4→v5→b=12 发现a→v1→v4→v2=7权值最短 |
| 6 | 选入v2,此时S=<a、v3、v1、v4、v5、v2>
此时最短路径 a→a=0,a→v3=1,a→v1=2, a→v1→v4=3,a→v1→v4→v5=6, a→v1→v4→v2=7 以v2为中间点,从a→v1→v4→v2=7这条最短路径 开始找 |
U=<v6、b> a→v1→v4→v2→v6=9 a→v1→v4→v2→其他U中的顶点=∞ 发现a→v1→v4→v2→v6=9权值最短 |
| 7 | 选入v6,此时S=<a、v3、v1、v4、v5、v2、v6>
此时最短路径a→a=0,a→v3=1,a→v1=2, a→v1→v4=3,a→v1→v4→v5=6, a→v1→v4→v2=7,a→v1→v4→v2→v6=9 以v6为中间点,从a→v1→v4→v2→v6=9这条最短路径 开始找 |
U=<v6、b> a→v1→v4→v2→v6→b=11 发现a→v1→v4→v2→v6→b=11权值最短 |
| 8 | 选入b,此时S=<a、v3、v1、v4、v5、v2、v6、b>
此时最短路径a→a=0,a→v3=1,a→v1=2, a→v1→v4=3,a→v1→v4→v5=6, a→v1→v4→v2=7,a→v1→v4→v2→v6=9, a→v1→v4→v2→v6→b=11 |
U集合已空,算法结束。 |
其中每次步骤执行时,从S集合确定中间点和开始查找的最短路径,依次遍历U集合中的 点,遵循的原则是,按最短路径长度的递增次序依次把第二组的顶点加入S,保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度,在寻找最短权值时要注意查找前面步骤是否已经查找记录过。