数据挖掘实践（1）：基础理论（一）数学基础（一）向量与矩阵（一）向量基础

1 向量

1.1 什么是向量

指具有⼤⼩和⽅向的量，通常⽤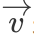来表示。

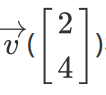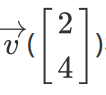如下图中的两个向量可以表示为 和

 

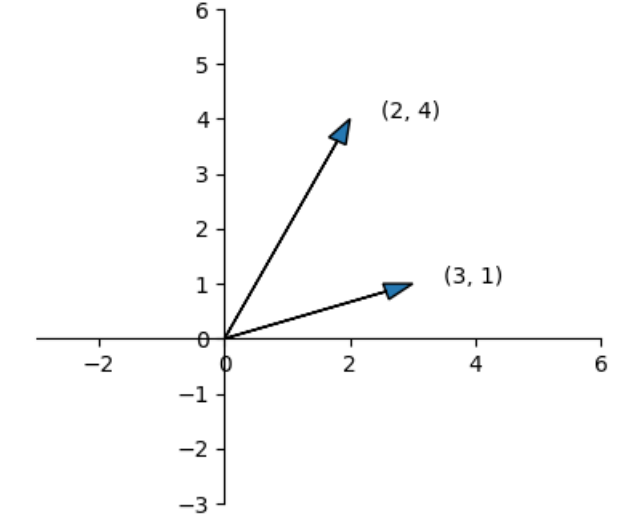
import numpy as np
np.array((2,4))

1.2 向量的计算⽅法

1.2.1 向量加减 

 

# 2+3 = 5
# 4+1 = 5
V = np.array((2,4))
U = np.array((3,1))
V-U

1.2.2 向量乘以常量

V = np.array((2,4))
V*1/3

1.2.3 向量的点乘（内积）

V = np.array((2,4))
U = np.array((3,1))
np.dot(V,U)

1.2.4 向量的叉乘（外积、向量积）

# V = [a1,a2,a3]
# U = [b1,b2,b3]
# P = [a2*b3,a3*b1-a1*b3,a1*b2-a2*b1]
V = np.array((1,2,3))
U = np.array((4,5,6))
# V*U 不对
# 2*6-3*5 = -3
np.cross(V,U)

1.2.5 向量的哈达玛积（Hadamard product）

V = np.array((2,4))
U = np.array((3,1))
V*U