数据挖掘实践（2）：基础理论（二）数学基础（二）向量与矩阵（二）矩阵

2 矩阵

2.1 什么是矩阵

在数学中：矩阵是⼀个按照⻓⽅阵列排列的复数或实数集合。

线性代数中：矩阵是描述线性代数中线性关系的参数，即矩阵是⼀个线性变换， 可以将⼀些向量转换为另⼀些向量。

import numpy as np
np.mat(np.random.randint(1,10,size = (3,4)))

2.2 矩阵的计算⽅法

2.2.1 矩阵的加减法

矩阵的加法与减法要求进⾏操作的两个矩阵A和B具有相同的阶， 假设矩阵A为m*n阶，矩阵B为m*n阶那么C=A+B|C=A-B也是m*n阶矩阵。

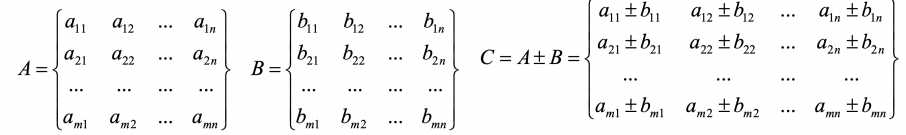
A = np.mat(np.random.randint(1,10,size=(3,4)))
B = np.mat(np.random.randint(1,10,size=(3,4)))
print(A)
print('-----')
print(B) A-B

2.2.2 矩阵与数的乘法

将数λ与矩阵A相乘，就是将数λ与矩阵A中的每⼀个元素相乘。

A = np.mat(np.random.randint(1,10,size=(3,4)))
print(A) A*1/3

2.2.3 矩阵与向量相乘

假设A为m*n阶矩阵，x为n*1的列向量，则Ax为m*1的列向量，计作：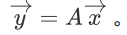

 

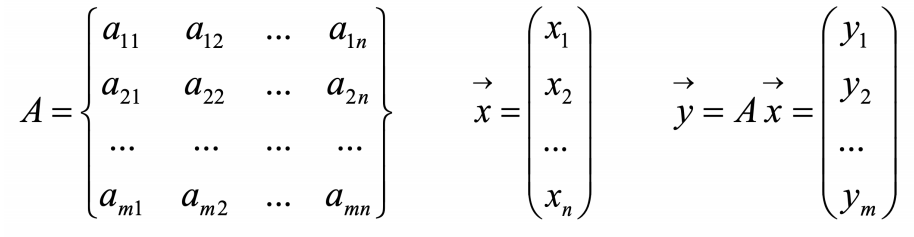
A = np.mat([[1,2,3],[4,5,6],[7,8,9]])
V = np.array([[2],[2],[2]])
print(A)
print(V) A*V

2.2.4 矩阵与矩阵相乘

矩阵的乘法仅当第⼀个矩阵A的列数和第⼆个矩阵B的⾏数相等时 才能够定义，假设A为m*s阶矩阵，B为s*n阶矩阵，那么C=A*B是m*n阶矩阵。

 

A = np.mat([[1,2],[3,4]])
B = np.mat([[1,2],[3,4]])
print(A)
print(B) A*B

np.multiply(A,B)

2.2.5 矩阵的转置

把矩阵A的⾏和列互相交换所产⽣的矩阵称为A的转置矩阵，这⼀过程叫做矩阵的转置。 ⽤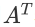表示。

 

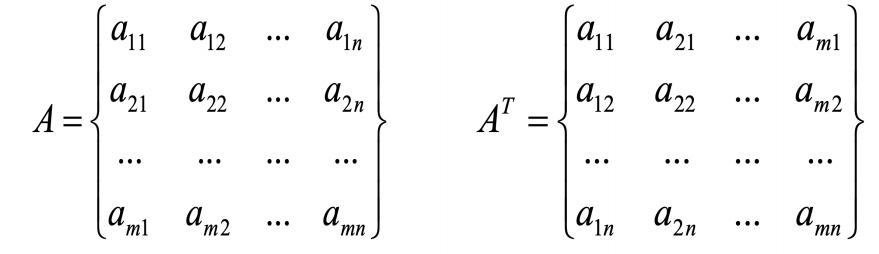
矩阵转置的⼏个性质

# A = np.mat([[1,2],[3,4]])
print(A)
# print('------')
# print(A.T)
# print('------')
# print(A.T.T)
# print((3*A).T)
# print(3*(A.T))
A = np.mat([[1,2,3],[4,5,6]])
B = np.mat([[1,2,3],[4,5,6]])
# print((A*B).T)
# print(B.T*A.T)
print((A+B).T)
print(A.T+B.T)

2.3 矩阵的导数

2.3.1 常⽤的导数

2.3.2 常⽤的矩阵导数

2.4 ⼏种特殊的矩阵

2.4.1 零矩阵

矩阵中各个元素全为0的矩阵。

import numpy as np
np.mat(np.zeros((3,4)))
np.mat(np.ones((3,4)))
np.mat(np.twos((3,4))) # x

2.4.2 单位矩阵

主对⻆线上的元素都是1，其他元素都是0的矩阵。

np.identity(4)

2.4.3 对⻆矩阵

主对⻆线之外的元素皆为0的矩阵

np.diag((1,2,3,4))

2.4.4 对称矩阵

是指以主对⻆线为对称轴，各元素对应相等的矩阵

对称矩阵的⼀个性质：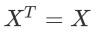

X = np.mat([[1,2,3],[4,5,6],[7,8,9]])
A = np.triu(X) X = A+A.T-np.diag((np.diagonal(X)))
print(X)

2.4.5 正交矩阵

如果矩阵满⾜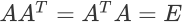（单位矩阵），则称该矩阵为正交矩阵。

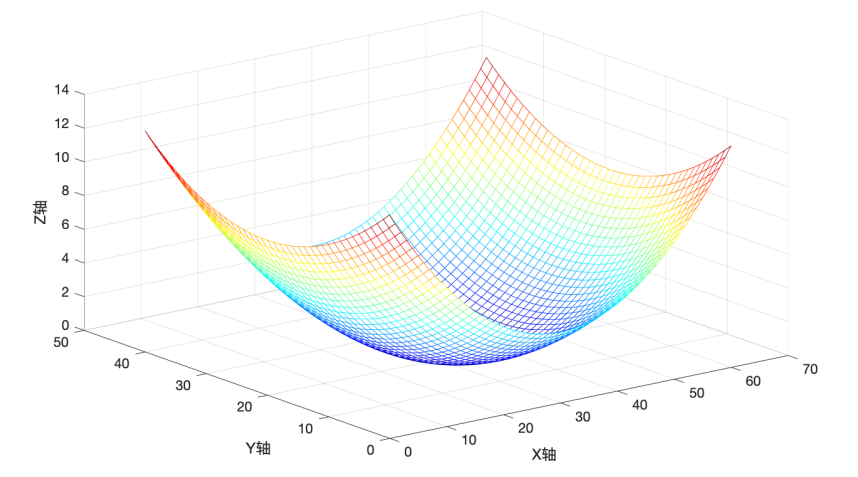
2.4.6 正定矩阵

 

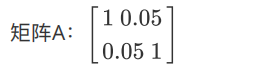
对应的空间曲⾯：

效果： 具有唯⼀的最⼩值。

2.4.7 半正定矩阵

 

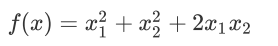
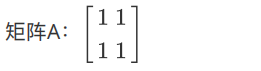
对应的空间曲⾯：

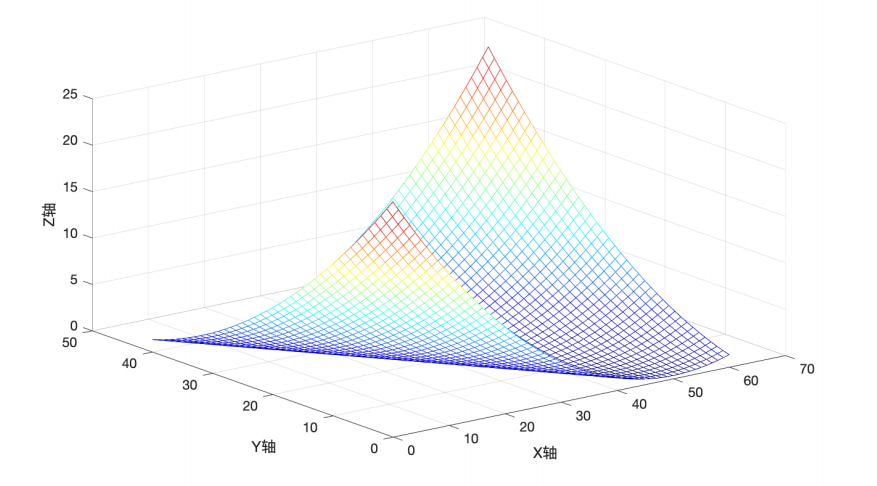
效果： 具有不唯⼀的最⼩值。

2.4.8 不定矩阵

 

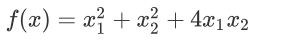
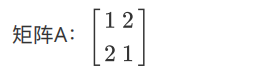
对应的空间曲⾯：

 

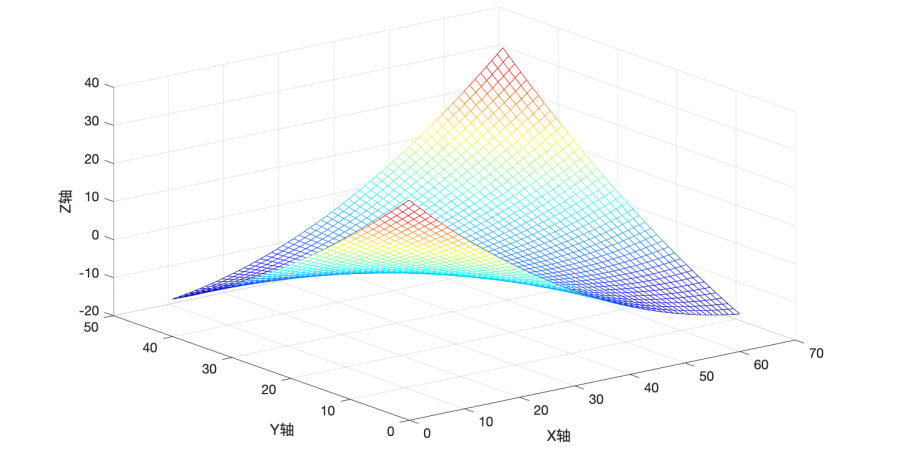
效果： 存在鞍点，⽆最⼩值点，也⽆最⼤值点。

2.4.9 负定矩阵

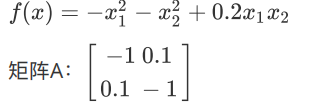
对应的空间曲⾯：

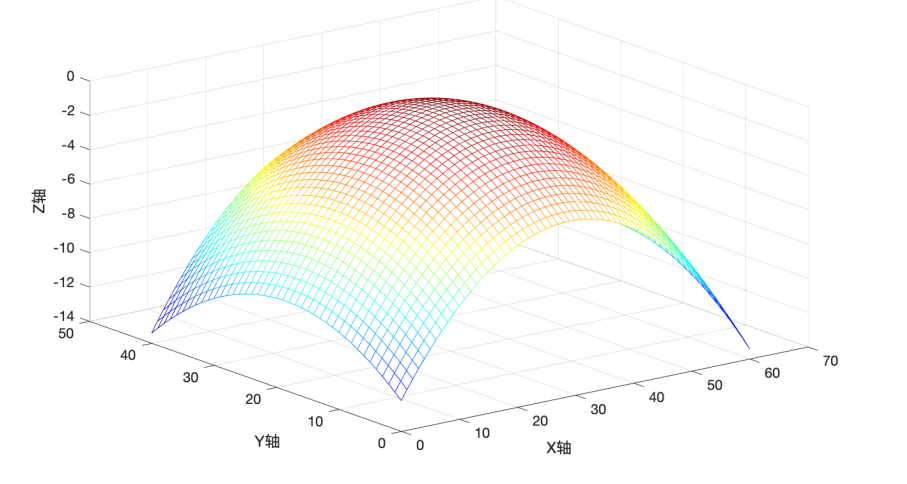
效果： 具有唯⼀的最⼤值。

2.4.10 半负定矩阵

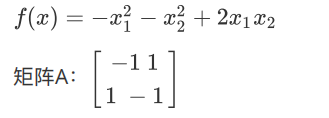
对应的空间曲⾯：

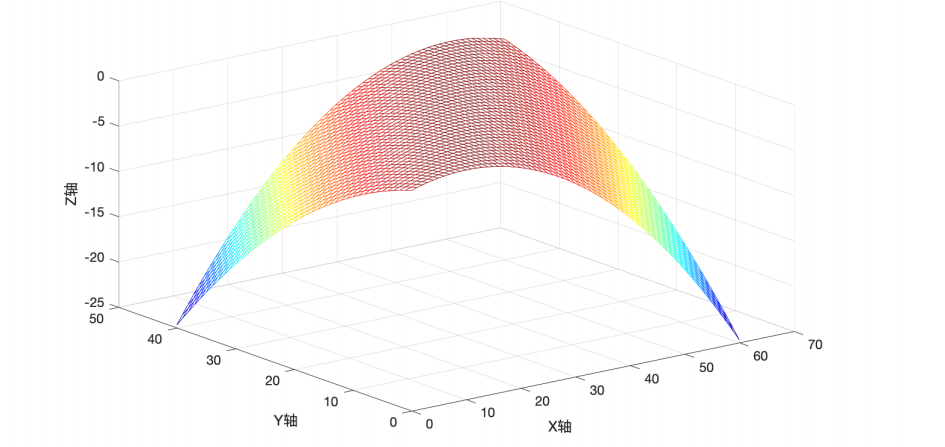
效果： 具有不唯⼀的最⼤值。

正定矩阵的⼏个性质：

定矩阵的⾏列式恒为正；

实对称矩阵A正定当且仅当A与单位矩阵合同；

两个正定矩阵的和是正定矩阵；

正实数与正定矩阵的乘积是正定矩阵。