数据挖掘实践（20）：算法基础（三）SVM(支持向量机)算法

1 基本函数确立

1.1 SVM的由来

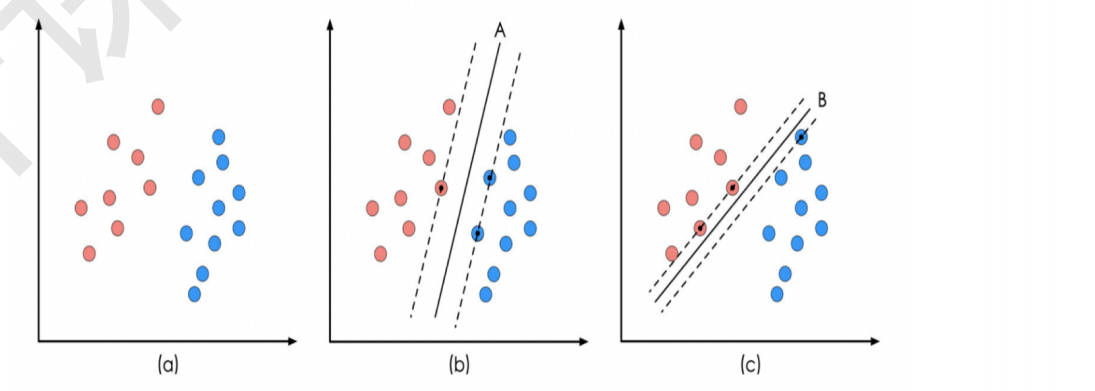
　　SVM 算法认为图中的分类器 A 在性能上优于分类器 B ，其依据是 A 的分类间隔比 B 要大。这里涉及到第一个 SVM 独有的概念“分类间隔”。

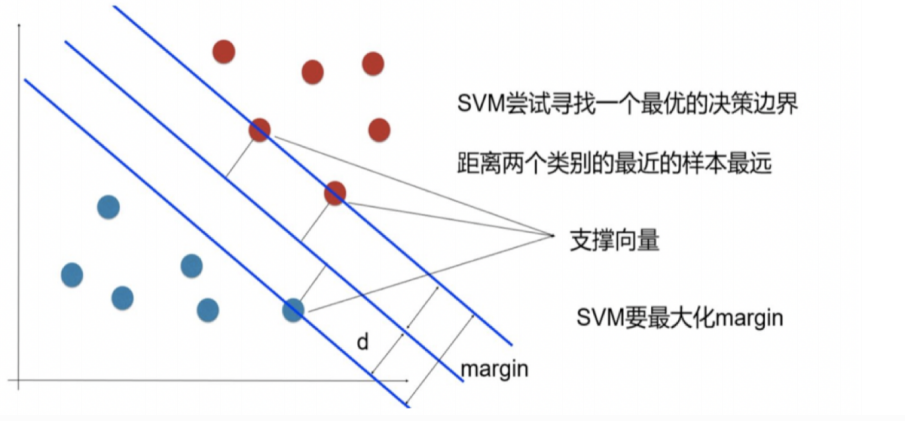
　　在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位，就会产生错分现象），如虑线所示。虚线的位，由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。显然每一个可能把数据集正确分开的方向都有一个最优决策面 (有些方向无论如何移动决策面的位置也不可能将两类样本完全分开），而不同方向的最优决策面的分类间隔通常是不同的，那个具有“最大间隔”的决策面就是 SVM 要寻找的最优解。而这个真正的最优解对应的两侧虑线所穿过的样本点，就是 SVM 中的支持样本点，称为“支持向量”。对于图中的数据， A 决策面就是 SVM 寻找的最优解．而相应的三个位于虚线上的样本点在坐标系中对应的向量．就叫做支持向量。

1.2 线性支持向量机

 

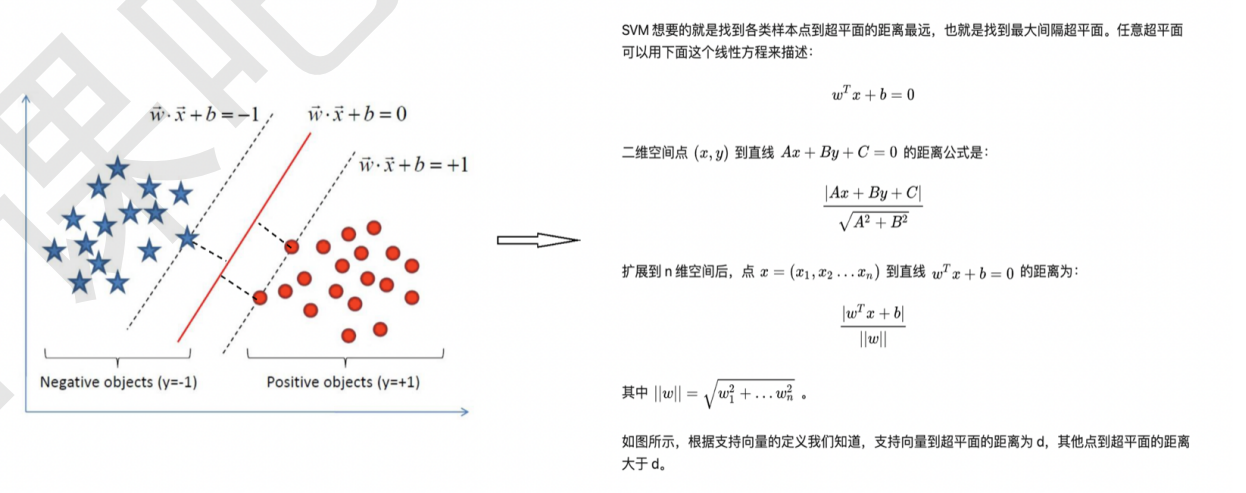
1.3 相关问题

　　关于”决策面”,为什么叫决策面，而不是决策线？

       样本是二维空间中的点，因此 1 维的直线可以分开它们。但是在更加一般的惰况下，样本点的维度是 n ，则将它们分开的决策面的维度就是 n -1 维的超平面（可以想象一下 3 维空间中的点集被平面分开）所以叫“决策面”更加具有普适性，或者你可以认为直线是决策面的一个特例。

      一个最优化问题通常有两个最基本的因素？都用哪些呢？

　　目标函数，也就是你希望什么东西的什么指标达到最好；

       优化对象，你期望通过改变哪些因素来使你的目标函数达到最优。在线性SVM算法中，目标函数显然就是那个“分类间隔”，而优化对象则是决策面。所以要对SVM问题进行数学建模，首先要对上述两个对象（“分类间隔”和“决策面”）进行数学描述

1.4 代码实验

# 导入必要的包
%matplotlib inline 
import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats

# 引入数据集，并可视化
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=50, centers=2,
                  random_state=0, cluster_std=0.60)
plt.figure(figsize=(8,8))
plt.scatter(X[:, 0], X[:, 1], c=y, s=50);

#要完成一个分类问题，需要在2种不同的样本点之间产出一条“决策边界”，下图显示了3条不同的可选决策边界。
xfit = np.linspace(-1, 3.5)
plt.figure(figsize=(8,8))

plt.scatter(X[:, 0], X[:, 1], c=y, s=50)

for k, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
#     print('k 	'+str(k))
#     print('b 	'+str(b))
#     print("-------------")
    
    plt.plot(xfit, k * xfit + b, '-k')

plt.xlim(-1, 3.5);

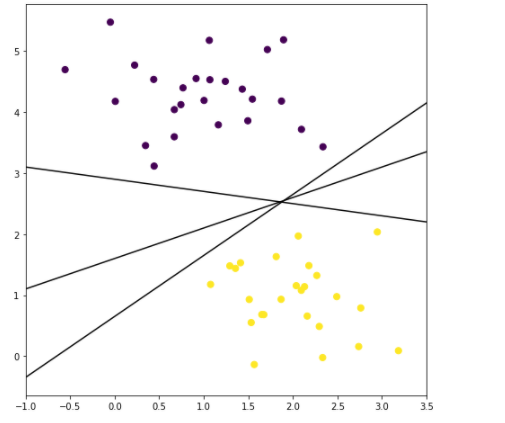
#SVM中的最初思想，就是找到一个分类器，能得到上图里在中间位置的，能有最大分类间隔的决策边界
#拟合支持向量机，这是一个线性可切分的例子，用sklearn中linear kernel的svm来分一下。
#构建一个线性SVM分类器
from sklearn.svm import SVC # "Support Vector Classifier"

clf = SVC(kernel='linear')
clf.fit(X, y)

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
    kernel='linear', max_iter=-1, probability=False, random_state=None,
    shrinking=True, tol=0.001, verbose=False)

# 可视化函数
def plot_svc_decision_function(clf, ax=None):
    """Plot the decision function for a 2D SVC"""
    if ax is None:
        ax = plt.gca()
    x = np.linspace(plt.xlim()[0], plt.xlim()[1], 30)
    y = np.linspace(plt.ylim()[0], plt.ylim()[1], 30)
    Y, X = np.meshgrid(y, x)
    P = np.zeros_like(X)
    for i, xi in enumerate(x):
        for j, yj in enumerate(y):
            P[i, j] = clf.decision_function([[xi, yj]])
    # plot the margins
    ax.contour(X, Y, P, colors='k',
               levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--'])

plt.figure(figsize=(8,8))
plt.scatter(X[:, 0], X[:, 1], c=y, s=50)
plot_svc_decision_function(clf);

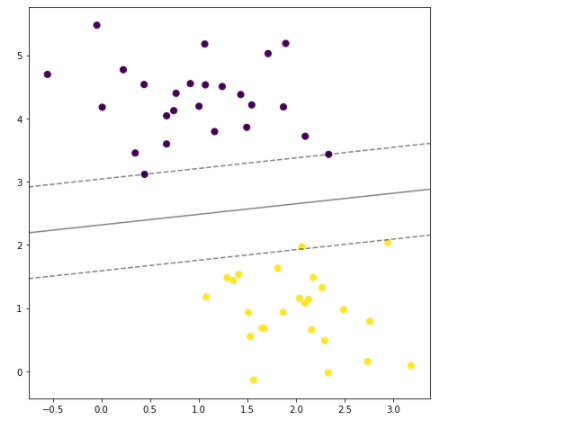
2.确立目标函数

 

 

 

3 确立最优函数

3.1 数学分析工具:拉格朗日乘之法

 

 对偶函数计算

 

 3.2 线性可分支持向量机算法

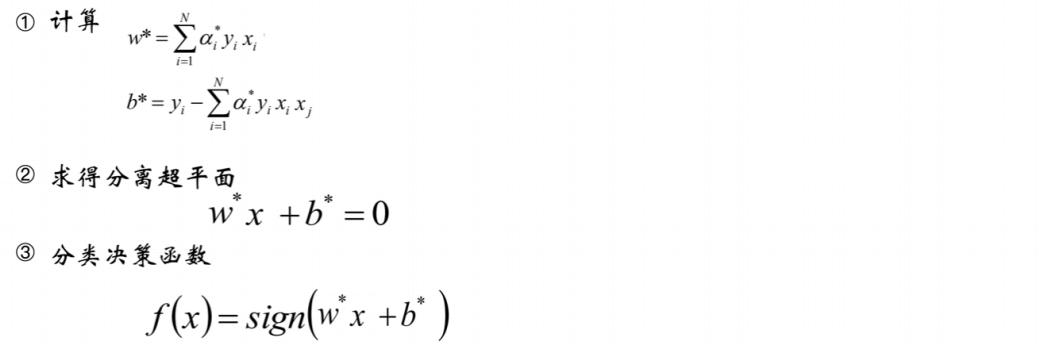
 3.3 拉格朗日算法思路

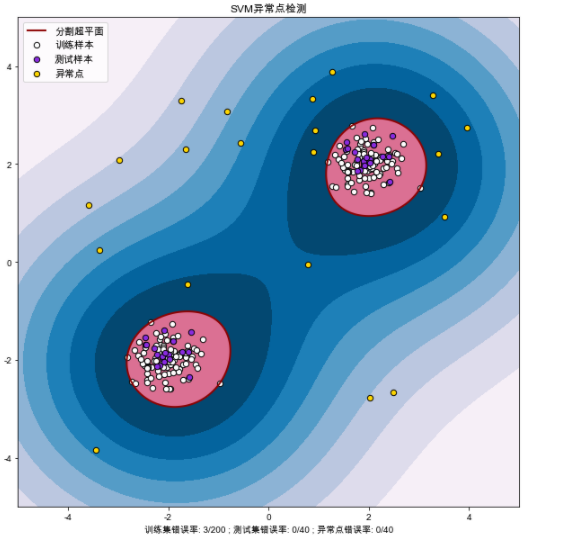
 4 SVM实践：异常值的检测

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib.font_manager
from sklearn import svm

• 自定义一些数据，其中90%是正常的数据，10%是非正常的数据，或者叫做离群点，用SVM测试一下

# 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] #Mac自带的字体
mpl.rcParams['axes.unicode_minus'] = False

# 模拟数据产生：横轴有500个样本，纵轴上有500个样本形成了网格(meshigrid)
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# 产生训练数据
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# 产测试数据
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# 产生一些异常点数据：最小值是-4，最大值是4的异常数据；uniform是一致的意思
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))

# 模型训练：OneClassSVM是一个类别的模型 ； nu:允许模型错误0.1% ，rbf是高斯核函数
clf = svm.OneClassSVM(nu=0.01, kernel="rbf", gamma=0.1)
clf.fit(X_train)

OneClassSVM(cache_size=200, coef0=0.0, degree=3, gamma=0.1, kernel='rbf',
            max_iter=-1, nu=0.01, random_state=None, shrinking=True, tol=0.001,
            verbose=False)

# 预测结果获取
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers) #异常值预测
# 返回1表示属于这个类别，-1表示不属于这个类别
n_error_train = y_pred_train[y_pred_train == -1].size # 在训练集上返回-1的数据，就是错误的  
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size

%matplotlib inline
# 获取绘图的点信息
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 画图
plt.figure(facecolor='w' , figsize=(10,10))
plt.title("SVM异常点检测")
# 画出区域图：Z是500*500 ，levels：是等级的意思，9层 ，越往里越分的对，越往外越分错了
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 9), cmap=plt.cm.PuBu)
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')#levels=[0]是红色，最里面的全
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred')

# 画出点图
s = 40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s, edgecolors='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='blueviolet', s=s, edgecolors='k')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='gold', s=s, edgecolors='k')

# 设置相关信息
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a.collections[0], b1, b2, c],
           ["分割超平面", "训练样本", "测试样本", "异常点"],
           loc="upper left",
           prop=matplotlib.font_manager.FontProperties(size=11))
plt.xlabel("训练集错误率: %d/200 ; 测试集错误率: %d/40 ; 异常点错误率: %d/40" 
           % (n_error_train, n_error_test, n_error_outliers))
plt.show()