机器学习sklearn（十五）： 特征工程（六）特征选择（一）主成分分析PCA

1. 准确的PCA和概率解释（Exact PCA and probabilistic interpretation）

PCA 用于对具有一组连续正交分量(Orthogonal component 译注: 或译为正交成分,下出现 成分 和 分量 是同意词)的多变量数据集进行方差最大化的分解。 在 scikit-learn 中， PCA 被实现为一个变换器对象， 通过 fit 方法可以拟合出 n 个成分， 并且可以将新的数据投影(project, 亦可理解为分解)到这些成分中。

在应用SVD(奇异值分解) 之前, PCA 是在为每个特征聚集而不是缩放输入数据。可选参数 whiten=True 使得可以将数据投影到奇异（singular）空间上，同时将每个成分缩放到单位方差。 如果下游模型对信号的各向同性作出强假设，这通常是有用的，例如，使用RBF内核的 SVM 算法和 K-Means 聚类算法。

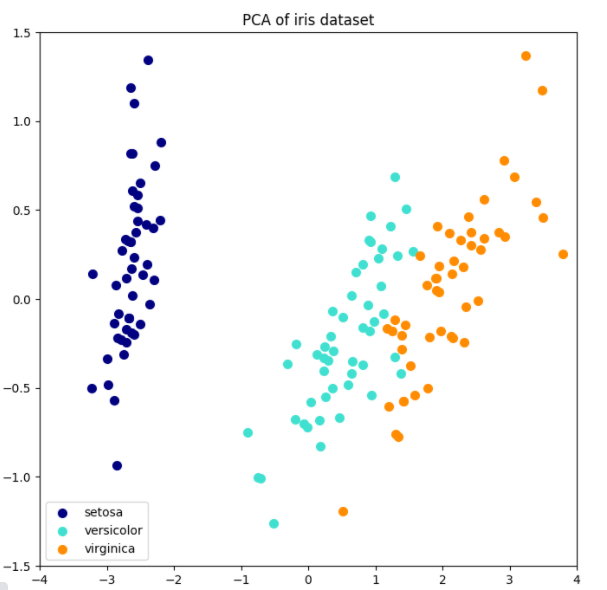
以下是iris数据集的一个示例，该数据集包含4个特征，通过PCA降维后投影到方差最大的二维空间上：

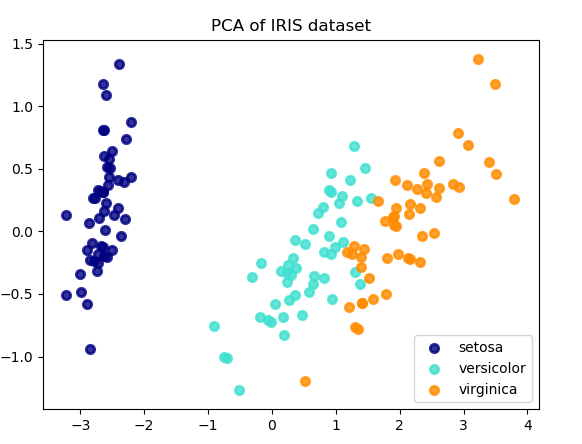
PCA 对象还提供了 PCA 算法的概率解释，其可以基于可解释的方差量给出数据的可能性。PCA对象实现了在交叉验证（cross-validation）中使用 score 方法：

 

示例:

• Comparison of LDA and PCA 2D projection of Iris dataset
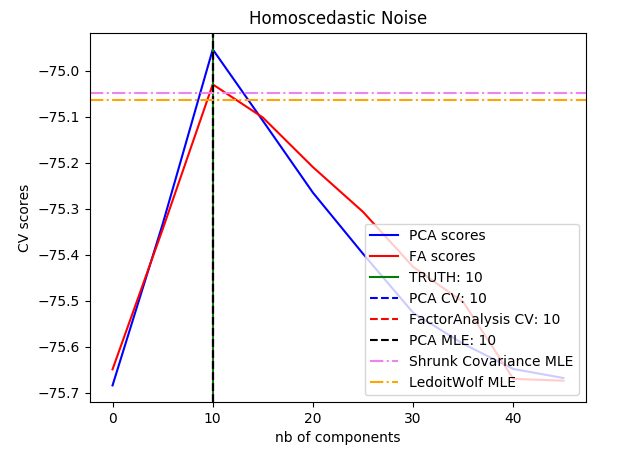
• Model selection with Probabilistic PCA and Factor Analysis (FA)

2. 增量PCA (Incremental PCA)

PCA 对象非常有用, 但 针对大型数据集的应用, 仍然具有一定的限制。 最大的限制是 PCA 仅支持批处理，这意味着所有要处理的数据必须放在主内存。 IncrementalPCA 对象使用不同的处理形式, 即允许部分计算以小型批处理方式处理数据的方法进行, 而得到和 PCA 算法差不多的结果。 IncrementalPCA 可以通过以下方式实现核外（out-of-core）主成分分析：

• 基于从本地硬盘或网络数据库中连续获取的数据块之上, 使用 partial_fit 方法。
• 在 memory mapped file (通过 numpy.memmap 创建)上使用 fit 方法。

IncrementalPCA 类为了增量式的更新 explainedvariance_ratio ，仅需要存储估计出的分量和噪声方差。 这就是为什么内存使用量依赖于每个批次的样本数量，而不是数据集中需要处理的样本总量。

在应用SVD之前，IncrementalPCA就像PCA一样,为每个特征聚集而不是缩放输入数据。

 

示例

• Incremental PCA

3. 基于随机化SVD的PCA

通过丢弃具有较低奇异值的奇异向量的分量，将数据降维到低维空间并保留大部分方差信息是非常有意义的。

例如，如果我们使用64x64像素的灰度级图像进行人脸识别，数据的维数为4096，在这样大的数据上训练含RBF内核的支持向量机是很慢的。此外我们知道这些数据固有维度远低于4096，因为人脸的所有照片都看起来有点相似。样本位于较低维度的流体上（例如约200维）。 PCA算法可以用于线性变换数据，同时降低维数并同时保留大部分可描述的方差信息。

在这种情况下，使用可选参数 svd_solver='randomized' 的 PCA 是非常有用的。既然我们将要丢弃大部分奇异值，那么仅仅就实际转换中所需的奇异向量进行计算就可以使得 PCA 计算过程变得异常有效。

例如：以下显示了来自 Olivetti 数据集的 16 个样本肖像（以 0.0 为中心）。右侧是前 16 个奇异向量重画的肖像。因为我们只需要使用大小为  和  的数据集的前 16 个奇异向量, 使得计算时间小于 1 秒。

 

注意：使用可选参数 svd_solver='randomized' ，在 PCA 中我们还需要给出输入低维空间大小 n_components 。

我们注意到, 如果  且 , 对于PCA中的实现，随机 PCA 的时间复杂度是：, 而不是  。

就内部实现的方法而言, 随机 PCA 的内存占用量和 , 而不是  成正比。

注意：选择参数 svd_solver='randomized' 的 PCA 的 inverse_transform 的实现, 并不是对应 transform 的逆变换（即使 参数设置为默认的 whiten=False）

示例:

• Faces recognition example using eigenfaces and SVMs
• Faces dataset decompositions

参考资料:

• “Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions” Halko, et al., 2009

4. 核 PCA

KernelPCA 是 PCA 的扩展，通过使用核方法实现非线性降维（dimensionality reduction） (参阅 成对的矩阵, 类别和核函数)。 它具有许多应用，包括去噪, 压缩和结构化预测（ structured prediction ） (kernel dependency estimation（内核依赖估计）)。 KernelPCA 支持 transform 和 inverse_transform 。

 

示例:

• Kernel PCA

5. 稀疏主成分分析 ( SparsePCA 和 MiniBatchSparsePCA )

SparsePCA 是 PCA 的一个变体，目的是提取能最大程度得重建数据的稀疏分量集合。

小批量稀疏 PCA ( MiniBatchSparsePCA ) 是一个 SparsePCA 的变体，它速度更快但准确度有所降低。对于给定的迭代次数，通过迭代该组特征的小块来达到速度的增加。

Principal component analysis（主成分分析） (PCA) 的缺点在于，通过该方法提取的成分具有独占的密度表达式，即当表示为原始变量的线性组合时，它们具有非零系数，使之难以解释。在许多情况下，真正的基础分量可以被更自然地想象为稀疏向量; 例如在面部识别中，每个分量可能自然地映射到面部的某个部分。

稀疏的主成分产生更节约、可解释的表达式，明确强调了样本之间的差异性来自哪些原始特征。

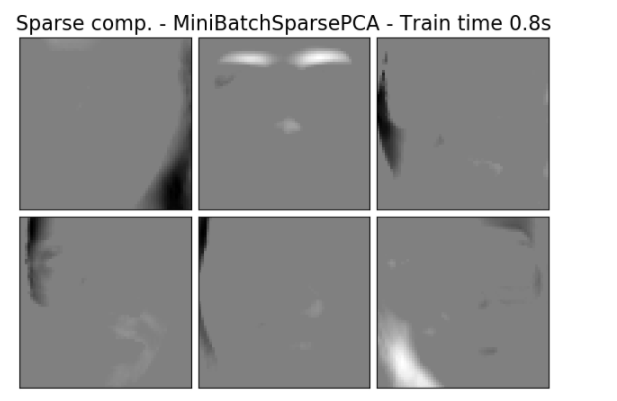
以下示例说明了使用稀疏 PCA 提取 Olivetti 人脸数据集中的 16 个分量。可以看出正则化项产生了许多零。此外，数据的自然结构导致了非零系数垂直相邻 （vertically adjacent）。该模型并不具备纯数学意义的执行: 每个分量都是一个向量 , 除非人性化地的可视化为 64x64 像素的图像，否则没有垂直相邻性的概念。下面显示的分量看起来局部化（appear local)是数据的内在结构的影响，这种局部模式使重建误差最小化。有一种考虑到邻接性和不同结构类型的导致稀疏的规范（sparsity-inducing norms）,参见 [Jen09] 对这种方法进行了解。有关如何使用稀疏 PCA 的更多详细信息，请参阅下面的示例部分。

 

 请注意，有多种不同的计算稀疏PCA 问题的公式。 这里使用的方法基于 [Mrl09] 。对应优化问题的解决是一个带有惩罚项（L1范数的）  的 PCA 问题（dictionary learning（字典学习））:

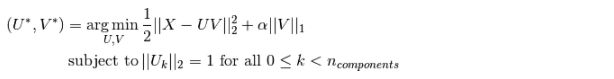
 稀疏推导（sparsity-inducing）  规范也可以当训练样本很少时,避免从噪声中拟合分量。可以通过超参数 alpha 来调整惩罚程度（或称稀疏度）。值较小会导致温和的正则化因式分解，而较大的值将许多系数缩小到零。

注意 虽然本着在线算法的精神， MiniBatchSparsePCA 类不实现 partial_fit , 因为在线算法是以特征为导向，而不是以样本为导向。

示例:

• Faces dataset decompositions

参考资料:

• [Mrl09] “Online Dictionary Learning for Sparse Coding” J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009
• [Jen09] “Structured Sparse Principal Component Analysis” R. Jenatton, G. Obozinski, F. Bach, 2009