机器学习sklearn（57）：算法实例（十四）分类（七）逻辑回归（二）linear_model.LogisticRegression(一) 重要参数

class sklearn.linear_model.LogisticRegression (penalty=’l2’, dual=False, tol=0.0001, C=1.0,fifit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’warn’, max_iter=100,multi_class=’warn’, verbose=0, warm_start=False, n_jobs=None)

1 二元逻辑回归的损失函数

1.1 损失函数的概念与解惑

 

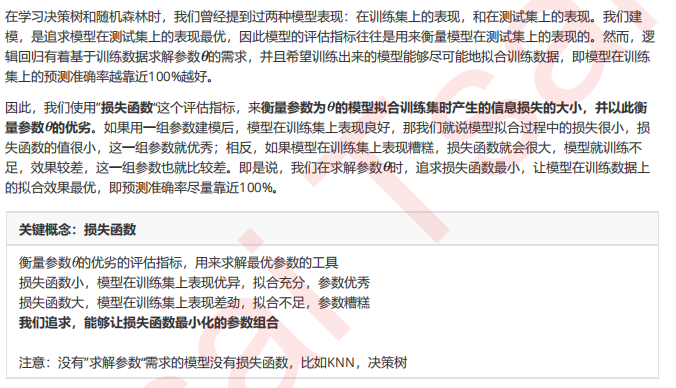
1.2【选学】二元逻辑回归损失函数的数学解释，公式推导与解惑 

 

 

 

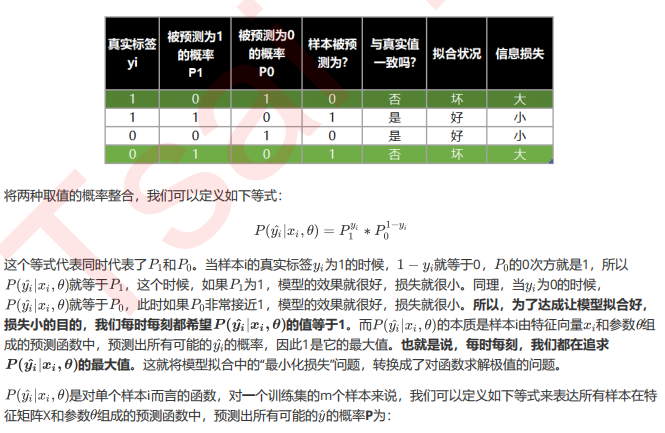
2 重要参数penalty & C 

2.1 正则化

 

 

from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
data = load_breast_cancer()
X = data.data
y = data.target
data.data.shape
lrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000) #逻辑回归的重要属性coef_，查看每个特征所对应的参数
lrl1 = lrl1.fit(X,y)
lrl1.coef_
(lrl1.coef_ != 0).sum(axis=1)
lrl2 = lrl2.fit(X,y)
lrl2.coef_

可以看见，当我们选择L1正则化的时候，许多特征的参数都被设置为了0，这些特征在真正建模的时候，就不会出现在我们的模型当中了，而L2正则化则是对所有的特征都给出了参数。

 

究竟哪个正则化的效果更好呢？还是都差不多？ 

l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.linspace(0.05,1,19):
    lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
    lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
    
    lrl1 = lrl1.fit(Xtrain,Ytrain)
    l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
    l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
    lrl2 = lrl2.fit(Xtrain,Ytrain)
    l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
    l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]    
plt.figure(figsize=(6,6))
for i in range(len(graph)):
    plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示，右下角
plt.show()

可见，至少在我们的乳腺癌数据集下，两种正则化的结果区别不大。但随着C的逐渐变大，正则化的强度越来越小，模型在训练集和测试集上的表现都呈上升趋势，直到C=0.8左右，训练集上的表现依然在走高，但模型在未知数据集上的表现开始下跌，这时候就是出现了过拟合。我们可以认为，C设定为0.8会比较好。在实际使用时，基本就默认使用l2正则化，如果感觉到模型的效果不好，那就换L1试试看。

2.2 逻辑回归中的特征工程 

 

高效的嵌入法embedded

from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel
data = load_breast_cancer()
data.data.shape
LR_ = LR(solver="liblinear",C=0.9,random_state=420)
cross_val_score(LR_,data.data,data.target,cv=10).mean()
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
X_embedded.shape
cross_val_score(LR_,X_embedded,data.target,cv=10).mean()

fullx = []
fsx = []
threshold = np.linspace(0,abs((LR_.fit(data.data,data.target).coef_)).max(),20) k=0
for i in threshold:
    X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(data.data,data.target)
    fullx.append(cross_val_score(LR_,data.data,data.target,cv=5).mean())
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=5).mean())
    print((threshold[k],X_embedded.shape[1]))
    k+=1
    
plt.figure(figsize=(20,5))
plt.plot(threshold,fullx,label="full")
plt.plot(threshold,fsx,label="feature selection")
plt.xticks(threshold)
plt.legend()
plt.show()

然而，这种方法其实是比较无效的，大家可以用学习曲线来跑一跑：当threshold越来越大，被删除的特征越来越多，模型的效果也越来越差，模型效果最好的情况下需要保证有17个以上的特征。实际上我画了细化的学习曲线，如果要保证模型的效果比降维前更好，我们需要保留25个特征，这对于现实情况来说，是一种无效的降维：需要30个指标来判断病情，和需要25个指标来判断病情，对医生来说区别不大。

2）第二种调整方法，是调逻辑回归的类LR_，通过画C的学习曲线来实现： 

fullx = []
fsx = []
C=np.arange(0.01,10.01,0.5)
for i in C:
    LR_ = LR(solver="liblinear",C=i,random_state=420)
    
    fullx.append(cross_val_score(LR_,data.data,data.target,cv=10).mean())
    
    X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())
    
print(max(fsx),C[fsx.index(max(fsx))])
plt.figure(figsize=(20,5))
plt.plot(C,fullx,label="full")
plt.plot(C,fsx,label="feature selection")
plt.xticks(C)
plt.legend()
plt.show()

继续细化学习曲线： 

fullx = []
fsx = []
C=np.arange(6.05,7.05,0.005)
for i in C:
    LR_ = LR(solver="liblinear",C=i,random_state=420)
    
    fullx.append(cross_val_score(LR_,data.data,data.target,cv=10).mean())
    
    X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())
    
print(max(fsx),C[fsx.index(max(fsx))])
plt.figure(figsize=(20,5))
plt.plot(C,fullx,label="full")
plt.plot(C,fsx,label="feature selection")
plt.xticks(C)
plt.legend()
plt.show()
#验证模型效果：降维之前
LR_ = LR(solver="liblinear",C=6.069999999999999,random_state=420)
cross_val_score(LR_,data.data,data.target,cv=10).mean()
#验证模型效果：降维之后
LR_ = LR(solver="liblinear",C=6.069999999999999,random_state=420)
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
cross_val_score(LR_,X_embedded,data.target,cv=10).mean()
X_embedded.shape

这样我们就实现了在特征选择的前提下，保持模型拟合的高效，现在，如果有一位医生可以来为我们指点迷津，看看剩下的这些特征中，有哪些是对针对病情来说特别重要的，也许我们还可以继续降维。当然，除了嵌入法，系数累加法或者包装法也是可以使用的。 

 

比较麻烦的系数累加法 

 

系数累加法的原理非常简单。在PCA中，我们通过绘制累积可解释方差贡献率曲线来选择超参数，在逻辑回归中我们可以使用系数coef_来这样做，并且我们选择特征个数的逻辑也是类似的：找出曲线由锐利变平滑的转折点，转折点之前被累加的特征都是我们需要的，转折点之后的我们都不需要。不过这种方法相对比较麻烦，因为我们要先对特征系数进行从大到小的排序，还要确保我们知道排序后的每个系数对应的原始特征的位置，才能够正确找出那些重要的特征。如果要使用这样的方法，不如直接使用嵌入法来得方便。

 

简单快速的包装法 

 

相对的，包装法可以直接设定我们需要的特征个数，逻辑回归在现实中运用时，可能会有”需要5~8个变量”这种需求，包装法此时就非常方便了。不过逻辑回归的包装法的使用和其他算法一样，并不具有特别之处，因此在这里就不在赘述，具体大家可以参考03期：数据预处理和特征工程中的代码。