机器学习sklearn（85）：算法实例（42）分类（21）朴素贝叶斯（四） 不同分布下的贝叶斯（三） 多项式朴素贝叶斯以及其变化

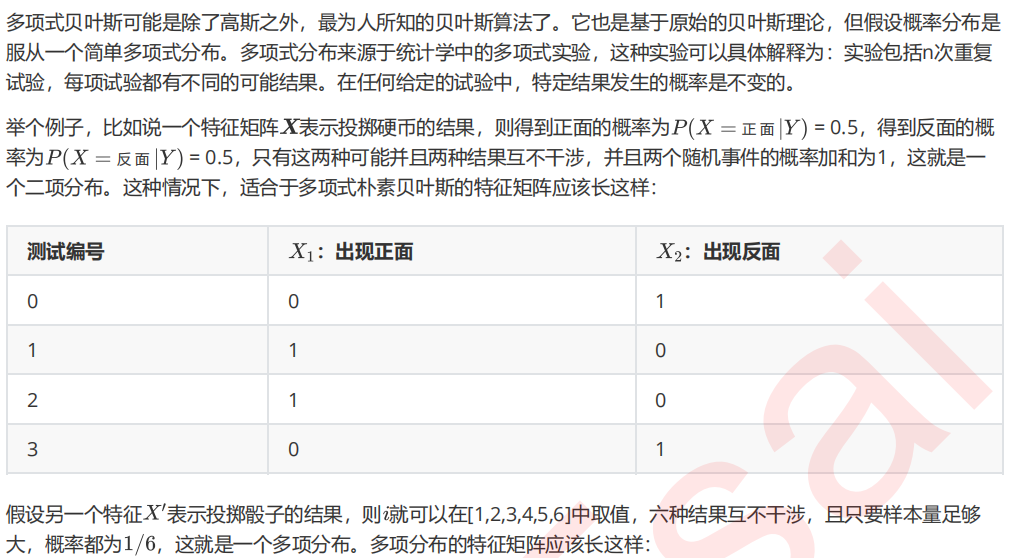
1 多项式朴素贝叶斯MultinomialNB

 

 

 

1. 导入需要的模块和库

from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.metrics import brier_score_loss

2. 建立数据集 

class_1 = 500
class_2 = 500 #两个类别分别设定500个样本
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [0.5, 0.5] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
                                               ,test_size=0.3
                                               ,random_state=420)

3. 归一化，确保输入的矩阵不带有负数

#先归一化，保证输入多项式朴素贝叶斯的特征矩阵中不带有负数
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)

4. 建立一个多项式朴素贝叶斯分类器吧

mnb = MultinomialNB().fit(Xtrain_, Ytrain) #重要属性：调用根据数据获取的，每个标签类的对数先验概率log(P(Y))
#由于概率永远是在[0,1]之间，因此对数先验概率返回的永远是负值
mnb.class_log_prior_
np.unique(Ytrain) (Ytrain == 1).sum()/Ytrain.shape[0]
mnb.class_log_prior_.shape
#可以使用np.exp来查看真正的概率值
np.exp(mnb.class_log_prior_) #重要属性：返回一个固定标签类别下的每个特征的对数概率log(P(Xi|y))
mnb.feature_log_prob_
mnb.feature_log_prob_.shape
#重要属性：在fit时每个标签类别下包含的样本数。当fit接口中的sample_weight被设置时，该接口返回的值也会受
到加权的影响
mnb.class_count_
mnb.class_count_.shape

5. 那分类器的效果如何呢？ 

#一些传统的接口
mnb.predict(Xtest_)
mnb.predict_proba(Xtest_)
mnb.score(Xtest_,Ytest)
brier_score_loss(Ytest,mnb.predict_proba(Xtest_)[:,1],pos_label=1)

7. 效果不太理想，思考一下多项式贝叶斯的性质，我们能够做点什么呢？

#来试试看把Xtiain转换成分类型数据吧
#注意我们的Xtrain没有经过归一化，因为做哑变量之后自然所有的数据就不会又负数了
from sklearn.preprocessing import KBinsDiscretizer
kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
Xtrain_ = kbs.transform(Xtrain)
Xtest_ = kbs.transform(Xtest)
mnb = MultinomialNB().fit(Xtrain_, Ytrain)
mnb.score(Xtest_,Ytest)
brier_score_loss(Ytest,mnb.predict_proba(Xtest_)[:,1],pos_label=1)

2 伯努利朴素贝叶斯BernoulliNB 

 

 

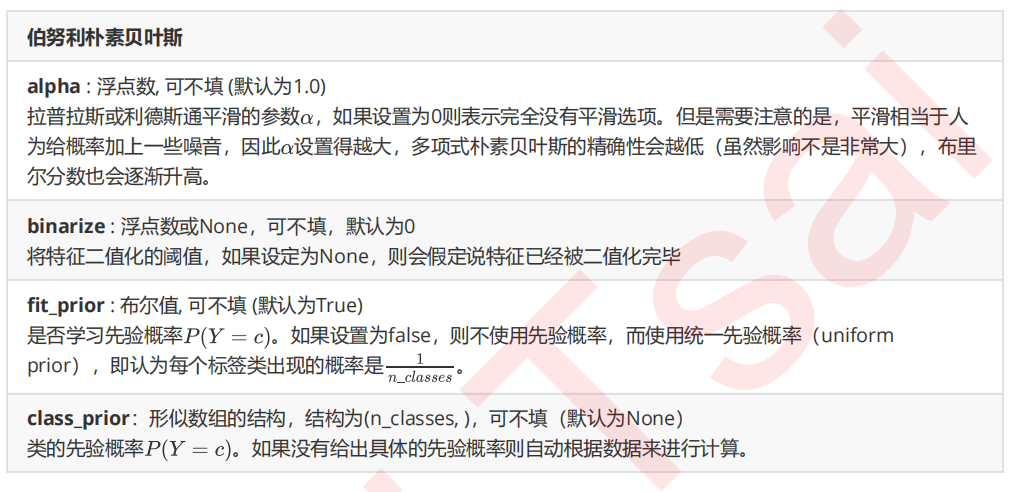
在sklearn中，伯努利朴素贝叶斯的实现也非常简单

from sklearn.naive_bayes import BernoulliNB
#普通来说我们应该使用二值化的类sklearn.preprocessing.Binarizer来将特征一个个二值化
#然而这样效率过低，因此我们选择归一化之后直接设置一个阈值
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest) #不设置二值化
bnl_ = BernoulliNB().fit(Xtrain_, Ytrain)
bnl_.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl_.predict_proba(Xtest_)[:,1],pos_label=1) #设置二值化阈值为0.5
bnl = BernoulliNB(binarize=0.5).fit(Xtrain_, Ytrain)
bnl.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl.predict_proba(Xtest_)[:,1],pos_label=1)

3 探索贝叶斯：贝叶斯的样本不均衡问题

1. 导入需要的模块，建立样本不平衡的数据集

from sklearn.naive_bayes import MultinomialNB, GaussianNB, BernoulliNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.metrics import brier_score_loss as BS,recall_score,roc_auc_score as AUC
class_1 = 50000 #多数类为50000个样本
class_2 = 500 #少数类为500个样本
centers = [[0.0, 0.0], [5.0, 5.0]] #设定两个类别的中心
clusters_std = [3, 1] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False) X.shape
np.unique(y)

2. 查看所有贝叶斯在样本不平衡数据集上的表现

name = ["Multinomial","Gaussian","Bernoulli"]
models = [MultinomialNB(),GaussianNB(),BernoulliNB()]
for name,clf in zip(name,models):
    Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
                                               ,test_size=0.3
                                               ,random_state=420)
    if name != "Gaussian":
        kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
        Xtrain = kbs.transform(Xtrain)
        Xtest = kbs.transform(Xtest)
    
    clf.fit(Xtrain,Ytrain)
    y_pred = clf.predict(Xtest)
    proba = clf.predict_proba(Xtest)[:,1]
    score = clf.score(Xtest,Ytest)
    print(name)
    print("	Brier:{:.3f}".format(BS(Ytest,proba,pos_label=1)))
    print("	Accuracy:{:.3f}".format(score))
    print("	Recall:{:.3f}".format(recall_score(Ytest,y_pred)))
    print("	AUC:{:.3f}".format(AUC(Ytest,proba)))

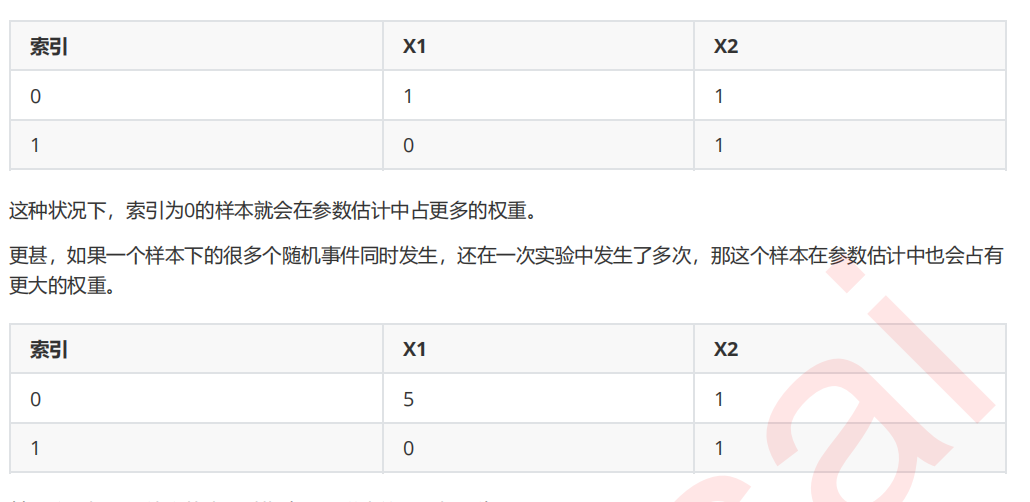
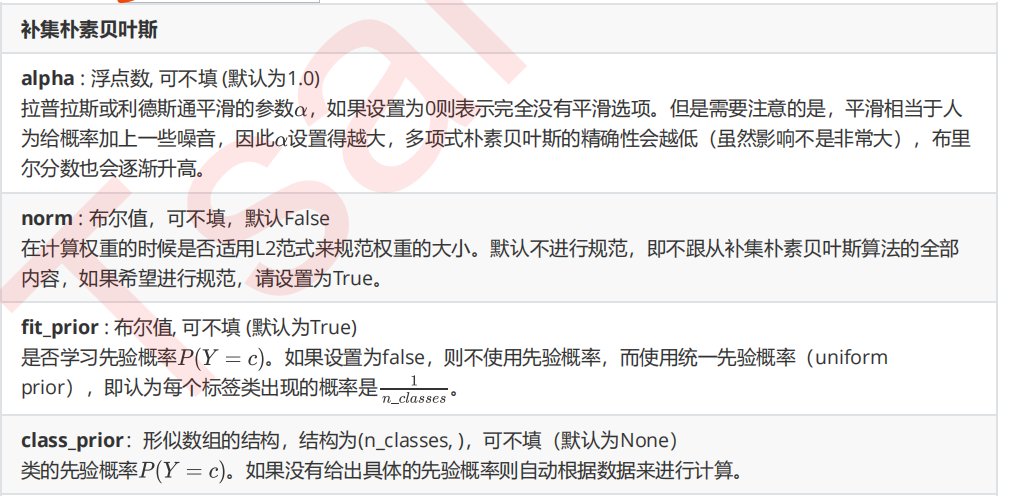
4 改进多项式朴素贝叶斯：补集朴素贝叶斯ComplementNB

 

 

 

 

 

from sklearn.naive_bayes import ComplementNB
from time import time
import datetime
name = ["Multinomial","Gaussian","Bernoulli","Complement"]
models = [MultinomialNB(),GaussianNB(),BernoulliNB(),ComplementNB()]
for name,clf in zip(name,models):
    times = time()
    Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
                                               ,test_size=0.3
                                               ,random_state=420)
    #预处理
    if name != "Gaussian":
        kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
        Xtrain = kbs.transform(Xtrain)
        Xtest = kbs.transform(Xtest)
    
    clf.fit(Xtrain,Ytrain)
    y_pred = clf.predict(Xtest)
    proba = clf.predict_proba(Xtest)[:,1]
    score = clf.score(Xtest,Ytest)
    print(name)
    print("	Brier:{:.3f}".format(BS(Ytest,proba,pos_label=1)))
    print("	Accuracy:{:.3f}".format(score))
    print("	Recall:{:.3f}".format(recall_score(Ytest,y_pred)))
    print("	AUC:{:.3f}".format(AUC(Ytest,proba)))
    print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))