1. 古板的定义
马尔可夫链因俄国数学家Andrey Andreyevich Markov得名,为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。马尔科夫链作为实际过程的统计模型具有许多应用。
看完这个定义我的表情是下面这样的

看过大佬的一些通俗解释的例子: 假如每天的天气是一个状态: 比如昨天是阴天, 今天是晴天,则明天的天气是什么只和今天的天气(晴天)有关,和今天之前的任何天气都没有关系.(就是当前的状态只和前一个状态有关系,和别的任何状态都无关)
所以根据定义可以知道数学定义的公式如下:

2. 举个例子解释马尔可夫链

这个例子是参考一个博客的:(链接等下我会发在底部)
这个例子是用来描述股市如下图:

总共是三个状态: Bull market: 表示牛市 Bear market 表示熊市 Stagnant表示横盘
接下来根据图我们可以定义状态转移矩阵
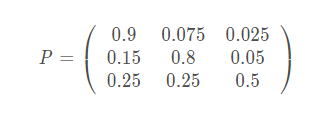
从一个状态转移为另一个状态的表示为P(i,j) 表示从状态 i 转变为状态 j 的概率 其中Bull market 表示为状态 0 Bear market 表示为状态1 Stagnant表示为状态2
接下来是一个有意思的事情:
我们假设现在的市场是牛市: 状态矩阵为[1,0,0]
import numpy as np def markov(): init_array = np.array([1,0,0]) transfer_matrix = np.array([[0.9, 0.075, 0.025], [0.15, 0.8, 0.05], [0.25, 0.25, 0.5]]) restmp = init_array for i in range(25): res = np.dot(restmp, transfer_matrix) print(res) restmp = res markov()
则输出的结果为:
1 [0.25 0.25 0.5 ] 2 [0.3875 0.34375 0.26875] 3 [0.4675 0.37125 0.16125] 4 [0.51675 0.372375 0.110875] 5 [0.54865 0.364375 0.086975] 6 [0.570185 0.3543925 0.0754225] 7 [0.585181 0.3451335 0.0696855] 8 [0.5958543 0.33741675 0.06672895] 9 [0.60356362 0.33130471 0.06513167] 10 [0.60918588 0.32659396 0.06422016] 11 [0.61331143 0.32301915 0.06366943] 12 [0.61635051 0.32033103 0.06331846] 13 [0.61859473 0.31832073 0.06308454] 14 [0.6202545 0.31682232 0.06292318] 15 [0.62148319 0.31570774 0.06280907] 16 [0.6223933 0.3148797 0.062727 ] 17 [0.62306768 0.31426501 0.06266732] 18 [0.62356749 0.31380891 0.0626236 ] 19 [0.62393798 0.31347059 0.06259143] 20 [0.62421263 0.31321968 0.0625677 ] 21 [0.62441624 0.31303361 0.06255015] 22 [0.62456719 0.31289565 0.06253716] 23 [0.62467911 0.31279335 0.06252754] 24 [0.62476209 0.3127175 0.06252042] 25 [0.62482361 0.31266126 0.06251514]
在第20次之后值就趋于一个固定的值 [0.62421263 0.31321968 0.0625677 ]
然后假设现在是熊市: 即状态为[0,1,0]
import numpy as np def markov(): init_array = np.array([0,1,0]) transfer_matrix = np.array([[0.9, 0.075, 0.025], [0.15, 0.8, 0.05], [0.25, 0.25, 0.5]]) restmp = init_array for i in range(25): res = np.dot(restmp, transfer_matrix) print(res) restmp = res markov()
结果如下:
1 [0.15 0.8 0.05] 2 [0.2675 0.66375 0.06875] 3 [0.3575 0.56825 0.07425] 4 [0.42555 0.499975 0.074475] 5 [0.47661 0.450515 0.072875] 6 [0.514745 0.4143765 0.0708785] 7 [0.5431466 0.3878267 0.0690267] 8 [0.56426262 0.36825403 0.06748335] 9 [0.5799453 0.35379376 0.06626094] 10 [0.59158507 0.34309614 0.06531879] 11 [0.60022068 0.33517549 0.06460383] 12 [0.60662589 0.3293079 0.06406621] 13 [0.61137604 0.32495981 0.06366415] 14 [0.61489845 0.32173709 0.06336446] 15 [0.61751028 0.31934817 0.06314155] 16 [0.61944687 0.3175772 0.06297594] 17 [0.62088274 0.31626426 0.062853 ] 18 [0.62194736 0.31529086 0.06276178] 19 [0.6227367 0.31456919 0.06269412] 20 [0.62332193 0.31403413 0.06264394] 21 [0.62375584 0.31363743 0.06260672] 22 [0.62407756 0.31334332 0.06257913] 23 [0.62431608 0.31312525 0.06255867] 24 [0.62449293 0.31296357 0.0625435 ] 25 [0.62462404 0.3128437 0.06253225]
在20次之后结果也会趋近一个值 [0.62407756 0.31334332 0.06257913]
通过使用转换矩阵,可以计算市场从持平到牛市所需的平均周数等。使用转换概率,稳态概率表明,在给定的周数中,62.5%的周将处于牛市中,31.25%的周将处于熊市中,6.25%的周将停滞,因为:
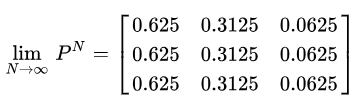
由此可知马尔科夫链又 细致平稳的性质(就是能收敛)
3.马尔可夫链细致平稳的条件
3.1 可能的状态数是有限的
3.2 状态间的转移概率需要不变( 状态转移矩阵不要变)
3.3 状态之间可以互相转换
3.4 状态不能是简单的循环 (比如状态是两个 互相循环)
针对3.4 举个例子:
假设只有两个状态互相循环转变:
import numpy as np def markov(): init_array = np.array([0,1]) restmp = init_array transfer_matrix1=[[0.1,0.2], [0.4,0.3]] for i in range(25): res = np.dot(restmp, transfer_matrix1) print(res) restmp = res markov()
得到结果如下:
1 [0.4 0.3] 2 [0.16 0.17] 3 [0.084 0.083] 4 [0.0416 0.0417] 5 [0.02084 0.02083] 6 [0.010416 0.010417] 7 [0.0052084 0.0052083] 8 [0.00260416 0.00260417] 9 [0.00130208 0.00130208] 10 [0.00065104 0.00065104] 11 [0.00032552 0.00032552] 12 [0.00016276 0.00016276] 13 [8.13802084e-05 8.13802083e-05] 14 [4.06901042e-05 4.06901042e-05] 15 [2.03450521e-05 2.03450521e-05] 16 [1.0172526e-05 1.0172526e-05] 17 [5.08626302e-06 5.08626302e-06] 18 [2.54313151e-06 2.54313151e-06] 19 [1.27156576e-06 1.27156576e-06] 20 [6.35782878e-07 6.35782878e-07] 21 [3.17891439e-07 3.17891439e-07] 22 [1.58945719e-07 1.58945719e-07] 23 [7.94728597e-08 7.94728597e-08] 24 [3.97364299e-08 3.97364299e-08] 25 [1.98682149e-08 1.98682149e-08]
会发现完全没有收敛
参考博客:
https://blog.csdn.net/bitcarmanlee/article/details/82819860
https://www.jiqizhixin.com/graph/technologies/fdebe132-cd51-43ba-8bda-a42abc478cbb