特征缩放 | 归一化和标准化 (下)

前面 特征缩放 | 归一化和标准化 (上) 简单介绍了 什么是特征缩放以及归一化，这里主要是涉及标准化 和一些特征缩放的总结。

什么是标准化？

标准化也是特征缩放的另外一种方式。它把数据归一到均值为0，方差为1的分布中。

如:

有一组样本

          (10个样本*3个特征)

将其标准化之后

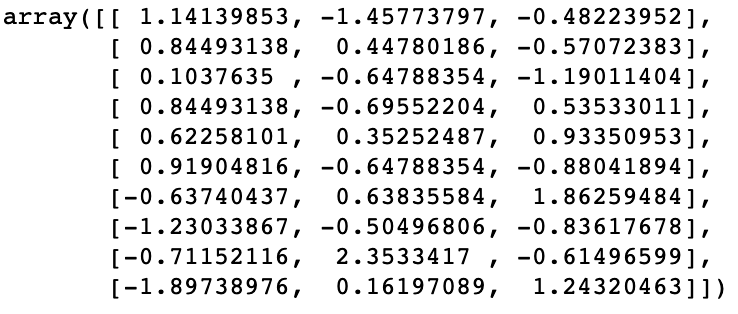
此时，特征1的均值为0，方差为1；特征2的均值为0，方差也为1。特征3如是

从计算结果的角度上看，标准化与归一化的区别在于:归一化之后所有数据被映射到0-1区间内。

而标准化之后，所有数据的均值为0，方差为1(以列为基准)

标准化公式:

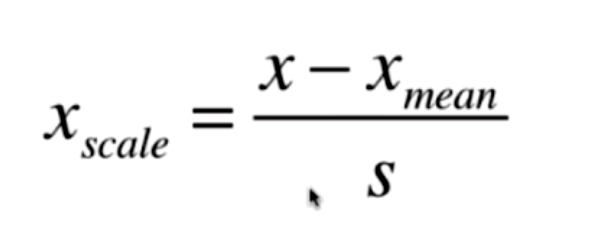
将特征值减去特征的均值 再除以特征的标准差

Python 简单实现

import numpy as np

def standard_scaler(X):
    '''标准化'''
    assert X.ndim == 2,'X muse be ....'

    n_feature = X.shape[1]

    for n in range(n_feature):
        n_mean =  np.mean(X[:,n])
        n_std = np.std(X[:,n])
        X[:,n] = (X[:,n] - n_mean) / n_std

    return X

x_samples = np.linspace(0,15,15).reshape(5,3) #生成样本数据
print('样本集:
',x_samples)
x_samples = standard_scaler(x_samples)
print('标准化:
',x_samples)

n_feature = x_samples.shape[1]
for n in range(n_feature):
    print('第{}列的均值{},方差{}'.format(n,np.mean(x_samples[:,n]),np.var(x_samples[:,n])))

 运行结果

样本集:
 [[ 0.          1.07142857  2.14285714]
 [ 3.21428571  4.28571429  5.35714286]
 [ 6.42857143  7.5         8.57142857]
 [ 9.64285714 10.71428571 11.78571429]
 [12.85714286 13.92857143 15.        ]]
标准化:
 [[-1.41421356e+00 -1.41421356e+00 -1.41421356e+00]
 [-7.07106781e-01 -7.07106781e-01 -7.07106781e-01]
 [ 1.95389284e-16  0.00000000e+00  0.00000000e+00]
 [ 7.07106781e-01  7.07106781e-01  7.07106781e-01]
 [ 1.41421356e+00  1.41421356e+00  1.41421356e+00]]
第0列的均值1.3322676295501878e-16,方差0.9999999999999997 
第1列的均值-4.4408920985006264e-17,方差0.9999999999999997
第2列的均值-4.4408920985006264e-17,方差0.9999999999999997

从运行结果上看，均值皆几乎接近于0，方差皆几乎接近于1



sklearn API:

from sklearn.preprocessing import StandardScaler

总结:

1.归一化的缩放与极值有关，所以容易受到极端值的干扰。其输出范围在[0,1]之间

2.标准化的缩放与均值、方差有关，其输出范围在负无穷到正无穷之间

3.当数据存在预测值或噪音时，可使用标准化