归并排序其实要做两件事:
(1)“分解”——将序列每次折半划分。
(2)“合并”——将划分后的序列段两两合并后排序。
具体过程如下图所示:

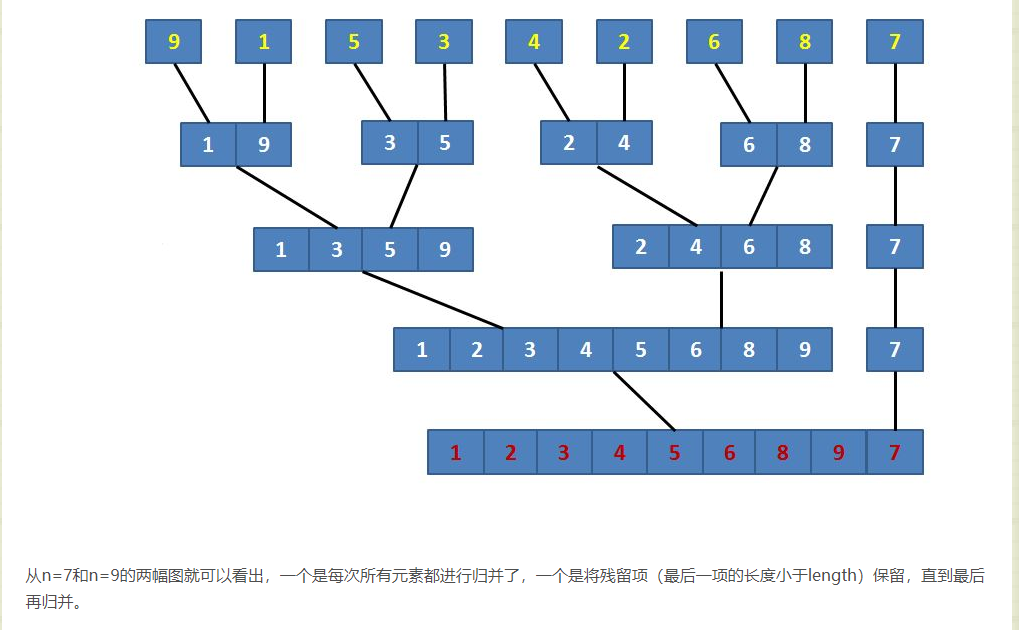
算法的时间复杂度是O(N*lgN),空间复杂度是O(N)。
本文会使用递归及非递归方式实现归并排序算法
递归版本
#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #include <stdio.h> typedef int RecType;//要排序元素类型 /// <summary> /// 将两个有序的子文件R[low..m)和R[m+1..high]归并成一个有序的子文件R[low..high] /// </summary> /// <param name="R">数组</param> /// <param name="low"></param> /// <param name="m">中间位置</param> /// <param name="high"></param> void Merge(RecType *R, int low, int m, int high) { //置初始值 p是新向量的计数 int i = low, j = m + 1, p = 0; RecType *R1; //R1是局部向量 R1 = (RecType *)malloc((high - low + 1)*sizeof(RecType)); //申请空间失败 if (!R1) { return; } //两子文件非空时取其小者输出到R1[p]上 while (i <= m&&j <= high) { R1[p++] = (R[i] <= R[j]) ? R[i++] : R[j++]; } //若第1个子文件非空,则复制剩余记录到R1中 while (i <= m) { R1[p++] = R[i++]; } //若第2个子文件非空,则复制剩余记录到R1中 while (j <= high) { R1[p++] = R[j++]; } //归并完成后将结果复制回R[low..high] for (p = 0, i = low; i <= high; p++, i++) { R[i] = R1[p]; } } void MergeSort(RecType R[], int low, int high) { //用分治法对R[low..high]进行二路归并排序 int mid; if (low<high) { //区间长度大于1 mid = (low + high) / 2; //分解 MergeSort(R, low, mid); //递归地对R[low..mid]排序 MergeSort(R, mid + 1, high); //递归地对R[mid+1..high]排序 Merge(R, low, mid, high); //组合,将两个有序区归并为一个有序区 } } void main() { int a[7] = { 49, 38, 65, 97, 76, 13, 27 }; //这里对7个元素进行排序 int low = 0, high = 6; //初始化low和high的值 printf("Before merge sort: "); for (int i = low; i <= high; i++) { printf("%d ", a[i]); //输出测试 } printf(" "); MergeSort(a, low, high); printf(" After merge sort: "); for (int i = low; i <= high; i++) { printf("%d ", a[i]); //输出测试 } printf(" "); }
非递归版
非递归版的归并排序,省略了中间的栈空间,直接申请一段O(n)的地址空间即可,因此空间复杂度为O(n),时间复杂度为O(nlogn);
#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #include <stdio.h> #include <time.h> int arrtest1[10] = {4,3,7,8,0,9,1,2,6,5}; int arrtest2[10] = {0,1,2,3,4,5,6,7,8,9}; int arrtest3[10] = {9,8,7,6,5,4,3,2,1,0}; void copy(int *from,int *arr,int length); void print(int *arr,int length); static void MergeSort(int *arr,int length); static void Merge(int *arr1,int *temp,int k,int length); void sort(int *arr,int *temp,int begin,int m,int end); int main(){ int Arr[10],i; copy(arrtest1,Arr,10); print(Arr,10); MergeSort(Arr,10); print(Arr,10); getchar(); return 0; } /// <summary> /// 以*2自增的归并方法 /// </summary> /// <param name="arr"></param> /// <param name="length">数组总长</param> void MergeSort(int *arr,int length){ //分配一个临时数组 int *temp = (int *)malloc(sizeof(int)*length); int i = 1; while(i<length){ Merge(arr,temp,i,length); i *= 2; } } /// <summary> /// /// </summary> /// <param name="arr1"></param> /// <param name="temp">temp数组</param> /// <param name="k">归并因子</param> /// <param name="length">总长度</param> void Merge(int *arr1,int *temp,int k,int length){ int i = 0,j; // while(i <= length-2*k){ //从i到i+2*k-1排序 sort(arr1,temp,i,i+k-1,i+2*k-1); //以2k为单位自增去排序 i += 2*k; } if(i < length-k+1)//如过剩余个数比一个k长度还多...那么就在进行一次合并 sort(arr1,temp,i,i+k-1,length-1); else for(j=i;j<length;j++) temp[j] = arr1[j]; //把temp的数据拷贝到原数组 for(i=0;i<length;i++){ arr1[i] = temp[i]; } } /// <summary> /// 实际进行排序的方法 temp为排序后的数组,然后在上个方法中统一拷贝到原数组 /// </summary> /// <param name="arr"></param> /// <param name="temp"></param> /// <param name="begin">开始位置</param> /// <param name="m">中间位置</param> /// <param name="end">结束位置</param> void sort(int *arr,int *temp,int begin,int m,int end){ //j=m+1 为后半区 j控制是否超限 //k为temp数组的索引游标 int i=begin,j=m+1,k,h; //判断条件为i小于中间位置且j小于结束位置 k位置每次加1 for(k=i; i<=m && j<=end;k++){ //判断开始位置和增量+1位置的大小,把较小的赋值给temp if(arr[i] < arr[j]) //j位置+1 temp[k] = arr[i++]; else temp[k] = arr[j++]; } if(i <= m){ for(h=0; h<=m-i;h++) temp[k+h] = arr[i+h]; }else{ for(h=0; h<=end-j;h++) temp[k+h] = arr[j+h]; } } /// <summary> /// /// </summary> /// <param name="from"></param> /// <param name="to"></param> /// <param name="length"></param> void copy(int *from,int *to,int length){ int i; for(i=0;i<length;i++){ to[i] = from[i]; } } void print(int *arr,int length){ int i; for(i=0;i<length;i++){ printf("%d ",arr[i]); } printf(" "); }